[14267] 회사 문화 1
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 | 512 MB | 11208 | 4301 | 3239 | 36.492% |
문제
영선회사에는 매우 좋은 문화가 있는데, 바로 상사가 직속 부하를 칭찬하면 그 부하가 부하의 직속 부하를 연쇄적으로 칭찬하는 내리 칭찬이 있다. 즉, 상사가 한 직속 부하를 칭찬하면 그 부하의 모든 부하들이 칭찬을 받는다.
모든 칭찬에는 칭찬의 정도를 의미하는 수치가 있는데, 이 수치 또한 부하들에게 똑같이 칭찬 받는다.
직속 상사와 직속 부하관계에 대해 주어지고, 칭찬에 대한 정보가 주어질 때, 각자 얼마의 칭찬을 받았는지 출력하시오,
입력
첫째 줄에는 회사의 직원 수 n명, 최초의 칭찬의 횟수 m이 주어진다. 직원은 1번부터 n번까지 번호가 매겨져 있다. (2 ≤ n, m ≤ 100,000)
둘째 줄에는 직원 n명의 직속 상사의 번호가 주어진다. 직속 상사의 번호는 자신의 번호보다 작으며, 최종적으로 1번이 사장이다. 1번의 경우, 상사가 없으므로 -1이 입력된다.
다음 m줄에는 직속 상사로부터 칭찬을 받은 직원 번호 i, 칭찬의 수치 w가 주어진다. (2 ≤ i ≤ n, 1 ≤ w ≤ 1,000)
사장은 상사가 없으므로 칭찬을 받지 않는다.
출력
1번부터 n번의 직원까지 칭찬을 받은 정도를 출력하시오.
문제풀이
이 문제는 직속 부하들의 연결 관계를 파악 후 칭찬을 기록하여 출력해주는 문제이다.
입력 및 필요한 변수 선언
상사와 부하를 연결하기 위해 tree 를 선언해주자.
상사를 입력 받으니 parents를 선언해주자.
칭찬을 출력해야 하니 like를 선언해주자.
static List<Integer> tree;
static int[] parents;
static int[] like;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
tree = new ArrayList[n + 1];
parents = new ArrayList[n + 1];
like = new ArrayList[n + 1];
}
트리 자료 구조를 이용하여 상사와 부하 관계 정의
입력은 직속상사의 노드 번호가 주어지는데 탐색은 상사 → 부하 방향으로 진행해야 하므로 트리로 자료를 저장한다.
for(int i = 1; i <= n; i++) {
tree[i] = new ArrayList<>();
parents[i] = sc.nextInt();
if(parents[i] == -1) return;
tree[parents[i]].add(i);
}
칭찬 기록하기
만약 모든 부하들을 찾아다니면서 동일 로직을 반복 탐색한다면 효율적이지 않다.
나에게 발생한 칭찬을 기록해 두고 모든 입력을 다 받은 뒤, 부하 직원에게 전달을 한다면 탐색 횟수를 줄일 수 있다.
칭찬을 받을 직원과 칭찬 점수를 입력 받아 like 배열에 있는 직원에 점수를 넣어주자.
for(int i = 0; i < m; i++) {
int employee = sc.nextInt();
int point = sc.nextInt();
like[employee] += point;
}
재귀를 통해 부하 직원에게 칭찬 점수 전달하기
like 배열에는 각 노드에 맞는 칭찬 점수를 저장했다.
이제 노드의 자식 노드에게 부모 노드의 칭찬 점수를 전달하여 자식 노드의 칭찬 점수 + 부모 노드의 칭찬 점수를 해줘야 한다.
즉, 자식 노드 = 자식 노드 + 부모 노드, 자식 노드 += 부모 노드 이다.
pulbic static void sumPoint(int node) {
for(int i = 0; i < tree[node].size(); i++) {
int child = tree[node].get(i);
like[child] += like[node];
sumPoint(child);
}
}
출력
like 배열에 값이 들어있을테니 이제 순회하며 출력해주자.
for(int i = 1; i <= n; i++)
System.out.print(like[i] + " ");
전체 코드
이 알고리즘의 시간복잡도는 O(n)이다.
import java.util.*;
class Main {
static List<Integer>[] tree;
static int[] parents;
static int[] like;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
tree = new ArrayList[n + 1];
parents = new int[n + 1];
like = new int[n + 1];
for (int i = 1; i <= n; i++) {
tree[i] = new ArrayList<>();
parents[i] = sc.nextInt();
if(parents[i] == -1) continue;
tree[parents[i]].add(i);
}
for (int i = 0; i < m; i++) {
int employee = sc.nextInt();
int point = sc.nextInt();
like[employee] += point;
}
sumPoint(1);
for(int i = 1; i <= n; i++)
System.out.print(like[i] + " ");
}
public static void sumPoint(int node) {
for (int i = 0; i < tree[node].size(); i++) {
int child = tree[node].get(i);
like[child] += like[node];
sumPoint(child);
}
}
}
[1068] 트리
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 | 128 MB | 69685 | 21138 | 15769 | 29.592% |
문제
트리에서 리프 노드란, 자식의 개수가 0인 노드를 말한다.
트리가 주어졌을 때, 노드 하나를 지울 것이다. 그 때, 남은 트리에서 리프 노드의 개수를 구하는 프로그램을 작성하시오. 노드를 지우면 그 노드와 노드의 모든 자손이 트리에서 제거된다.
예를 들어, 다음과 같은 트리가 있다고 하자.

현재 리프 노드의 개수는 3개이다. (초록색 색칠된 노드) 이때, 1번을 지우면, 다음과 같이 변한다. 검정색으로 색칠된 노드가 트리에서 제거된 노드이다.

이제 리프 노드의 개수는 1개이다.
입력
첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다. 셋째 줄에는 지울 노드의 번호가 주어진다.
출력
첫째 줄에 입력으로 주어진 트리에서 입력으로 주어진 노드를 지웠을 때, 리프 노드의 개수를 출력한다.
문제 풀이
이 문제는 리프 노드를 찾는 문제이다. 리프 노드란, 자식의 개수가 0인 노드이다.
하지만 어떠한 노드를 주었을때 그 노드가 루트인 서브 트리를 모두 제거해줘야 한다.
필요한 변수 선언 및 입력 받기
트리 구조를 사용하기 위해 트리 변수를 선언하자.
부모 노드를 입력 받기 위해 parent 변수를 선언하자.
중복 계산을 방지하기 위해 check 변수를 선언하자.
삭제할 노드 번호와 루트 노드도 선언하고
출력할 leatCount까지 선언하였다.
만약 부모 노드 입력값이 -1이면 루트 노드인것이다.
static List<Integer>[] tree;
static int[] parent;
static boolean[] check;
static int deleteNodeNum;
static int leafCount;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
tree = new ArrayList[n]; // 0부터 n-1까지 사용
for (int i = 0; i < n; i++) {
tree[i] = new ArrayList<>();
}
parent = new int[n];
check = new boolean[n];
int root = 0;
// 부모 노드 입력 및 트리 구성
for (int i = 0; i < n; i++) {
parent[i] = sc.nextInt();
if (parent[i] != -1) {
tree[parent[i]].add(i); // 부모 노드에 자식 추가
} else {
root = i; // 루트 노드 저장
}
}
deleteNodeNum = sc.nextInt(); // 삭제할 노드 번호
<---생략--->
리프 노드를 찾아보자.
만약 삭제할 노드가 root이면 0을 출력해주자.
findLeafNodes 함수를 실행하면 검사를 하였으니 check값을 업데이트 한다.
그리고 자식의 개수도 0으로 초기화 해주자.
그 이후 tree[node] 배열을 순회하며 제거하는 값이 아니고 검사하지 않았다면 자식이 있는 것이니 자식수를 증가하고 재귀를 해주자.
만약 자식이 없다는 것은 리프 노드이기에 리프노드 개수를 하나 증가 시켜 주자.
if (deleteNodeNum == root) {
System.out.println(0);
} else {
findLeafNodes(root);
System.out.println(leafCount);
}
public static void findLeafNodes(int node) {
check[node] = true;
int childCount = 0;
for (int child : tree[node]) {
if(child != deleteNodeNum && !check[child]) {
childCount++;
findLeafNodes(child);
}
}
if (childCount == 0) {
leafCount++;
}
}
전체 코드
이 알고리즘의 시간 복잡도는 O(n)이다.
import java.util.*;
class Main {
static List<Integer>[] tree;
static int[] parent;
static boolean[] check;
static int deleteNodeNum;
static int leafCount;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
tree = new ArrayList[n]; // 0부터 n-1까지 사용
for (int i = 0; i < n; i++) {
tree[i] = new ArrayList<>();
}
parent = new int[n];
check = new boolean[n];
int root = 0;
// 부모 노드 입력 및 트리 구성
for (int i = 0; i < n; i++) {
parent[i] = sc.nextInt();
if (parent[i] != -1) {
tree[parent[i]].add(i); // 부모 노드에 자식 추가
} else {
root = i; // 루트 노드 저장
}
}
deleteNodeNum = sc.nextInt(); // 삭제할 노드 번호
if (deleteNodeNum == root) {
System.out.println(0);
} else {
findLeafNodes(root);
System.out.println(leafCount);
}
}
public static void findLeafNodes(int node) {
check[node] = true;
int childCount = 0;
for (int child : tree[node]) {
if(child != deleteNodeNum && !check[child]) {
childCount++;
findLeafNodes(child);
}
}
if (childCount == 0) {
leafCount++;
}
}
}
[5639] 이진 검색 트리
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 1 초 | 256 MB | 52056 | 20627 | 14559 | 38.265% |
문제
이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.
- 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
- 노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
- 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
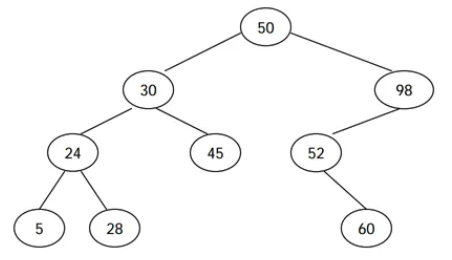
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.
이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.
입력
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.
출력
입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.
문제 풀이
이 문제를 풀려면 이진 트리의 특성을 알아야 한다.
이진 트리의 규칙은 아래와 같다.
- 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
- 노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
- 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
이진 트리를 전위 순회 한 값을 입력 값으로 주어진다.
그 값을 가지고 후위 순회 한 값을 출력하면 된다.
Node 클래스를 만들어 노드에 대한 자식 값을 넣어주자.
Node 클래스안에 프로퍼티는 int 타입인 value와 Node 타입인 left, right가 있다.
그리고 insert 재귀 함수가 있다.
만약 현재 노드의 값이 들어오는 값 보다 크다면 들어오는 값은 왼쪽에 위치해야 한다.
하지만 이미 들어온 값이 있다면 재귀를 통해 이미 들어온 값과 들어오는 값과 비교하여 왼쪽 오른쪽 어느쪽에 위치해야 할 지 정해주면 된다.
이 부분이 insert 메서드이다.
class Node {
int value;
Node left;
Node right;
Node(int num) {
this.value = num;
}
void insert(int n) {
if (n < this.value) {
if (this.left == null)
this.left = new Node(n);
else this.left.insert(n);
} else {
if (this.right == null)
this.right = new Node(n);
else this.right.insert(n);
}
}
}
후위 순회하여 출력하기
후위 순회를 하는 방식은 아래와 같다. left → right → root 순으로 출력 하면된다.
node의 left 자식이 있다면 계속 재귀하여 들어가고 없으면 출력하여 나온다.
public static void postOrder(Node node) {
if (node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.value);
}
전체 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
class Node {
int value;
Node left;
Node right;
Node(int num) {
this.value = num;
}
void insert(int n) {
if (n < this.value) {
if (this.left == null)
this.left = new Node(n);
else this.left.insert(n);
} else {
if (this.right == null)
this.right = new Node(n);
else this.right.insert(n);
}
}
}
class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
Node root = new Node(Integer.parseInt(br.readLine()));
String input;
while ((input = br.readLine()) != null) {
root.insert(Integer.parseInt(input));
}
postOrder(root);
}
public static void postOrder(Node node) {
if (node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.value);
}
}
'알고리즘 > Recursion' 카테고리의 다른 글
| [코딩테스트] [2529] 부등호 & [9095] 1,2,3 더하기 & [12101] 1,2,3 더하기 2 (1) | 2025.03.25 |
|---|---|
| [코딩테스트] [1759] 암호 만들기 & [10971] 외판원 순회 2 & [14888] 연산자 끼워넣기 (2) | 2025.02.19 |
| [코딩테스트] [1182] 부분수열의 합 & [2758] 로또 & [1208] 부분 수열의 합2 (0) | 2025.02.12 |
| [코딩테스트] [11725] 트리의 부모 찾기 & [1991] 트리 순회 & [15681] 트리와 쿼리 (0) | 2025.02.11 |
| [코딩테스트] 재귀함수 & [15654~15657] N과M (1) | 2025.02.07 |
