재귀함수
자기 자신을 호출하는 함수를 재귀함수라고 한다.
사용 이유
- 하나의 커다란 문제를 작은 문제로 나누어 해결하기 위해서
- 문제를 귀납적으로 생각하기 위해서
- 귀납적 예시, {i}번째 답을 구하기 위해 (i-1), (i-2), … 번째 결과를 활용한다.
예시
숫자 출력
오름차순과 내림차순을 재귀로 출력하는 방법을 봐 보자.
아래 사진을 보면 재귀를 통하여 출력되는 것을 볼 수 있다.

class Main {
static class PrintNumber {
public void asc (int n) {
if (n==0) return;
asc(n-1);
System.out.println(n);
}
public void desc(int n) {
if(n == 0) return;
System.out.println(n);
desc(n-1);
}
}
public static void main(String[] args) {
PrintNumber p = new PrintNumber();
p.asc(10);
p.desc(10);
}
}
Base Case
- 계산 없이 바로 답을 구할 수 있는 경우
- 재귀 호출을 멈추고 함수가 종료되는 조건 → 없다면 무한 루프에 빠지게 된다.
- 즉, 적어도 하나 이상의 Base Case가 있어야 한다.
Recursive Case
- 재귀 호출이 일어나는 경우
- 문제를 작은 부분으로 쪼개기 위함
- 함수가 호출될수록 부분 문제가 Base Case에 수렴해야 한다.
아래 이미지를 보면 if(n==0) return이 BaseCase가 되는 경우이고
자기 자신을 호출하는 부분이 asc(n-1)이 Recursive Case가 되는 경우이다.

[2747] 피보나치 수
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 1 초 (추가 시간 없음) | 128 MB | 83479 | 40401 | 33278 | 49.933% |
문제
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다.
이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다.
n=17일때 까지 피보나치 수를 써보면 다음과 같다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n이 주어진다. n은 45보다 작거나 같은 자연수이다.
출력
첫째 줄에 n번째 피보나치 수를 출력한다.
문제풀이
재귀함수의 예시중 대표적인 예로 피보나치 수가 있다.
이 문제의 BaseCase와 Recursive Case를 봐보자.
Base Case
계산없이 바로 답을 구하는 경우는 (n==1) || (n==2) 일때 이다.
Recursive Case
재귀 호출이 일어나는 경우는 fibo(n) = fibo(n-1) + fibo(n-2)이다.
static int fibo(int n) {
if (n == 1 || n == 2) return 1;
return fibo(n - 1) + fibo(n - 2);
}
// n값이 자연수 미만으로 내려가지 않도록 2번째 값까지
// BaseCase로 처리한다.
하지만 이렇게 코드를 제출하면 시간초과가 발생한다.

왜 시간초과가 발생하는 지 알아보자.
매개변수별 함수 호출 횟수를 보면 중복하여 연산이 되는 경우가 많다.

이것을 방지하기 위해 cache 배열을 만들어서 한번 계산이 된 경우라면 배열에 저장을 할 것이다.
import java.util.*;
class Main {
static int[] cached = new int[50];
static int fibo(int n) {
if (n==1|| n==2) return 1;
if (cached[n] != 0) return cached[n];
cached[n] = fibo(n-1) + fibo(n-2);
return cached[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(fibo(n));
}
}
[15654~15657] N과M
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 1 초 | 512 MB | 46435 | 33808 | 26860 | 72.257% |
문제
N개의 자연수와 자연수 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오. N개의 자연수는 모두 다른 수이다.
- N개의 자연수 중에서 M개를 고른 수열
입력
첫째 줄에 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)
둘째 줄에 N개의 수가 주어진다. 입력으로 주어지는 수는 10,000보다 작거나 같은 자연수이다.
출력
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다.
수열은 사전 순으로 증가하는 순서로 출력해야 한다.
문제풀이
15654부터 15657까지 재귀 함수를 이용하여 문제를 푸는 경우이다.
기본적인 베이스는 같고 조건이 조금씩 달라져 같이 풀이를 해보겠다.
15654 풀이
일단 이문제는 순열에 대해서 알아야 한다.
순열
- 집합 안에서 가능한 모든 조합을 나열하는 것을 순열이라고 한다.
- 특징
- 중복이 없는 n개의 원소 집합에서 n!개의 순열이 생성된다.
- 중복된 원소가 있는 경우 각 원소의{중복횟수!}의 곱으로 나눈 값의 개수만큼 순열이 생성된다.

N개의 자연수 집합에서 M개를 고른 수열을 사전순으로 출력한다.
중복되는 수열을 여러 번 출력하면 안된다.
사전순으로 출력하기 위해 집합의 숫자를 미리 사전 순으로 정렬하자.
public static int[] numbers;
public static int[] output;
public static boolean[] check;
public static int n;
public static int m;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
numbers = new int[n];
output = new int[m];
check = new boolean[n];
for (int i = 0; i < n; i++) {
numbers[i] = sc.nextInt();
}
Arrays.sort(numbers);
perm(0);
}
위의 코드를 보면 입력 받아야할 변수들과 필요한 배열들을 모두 초기화하였다.
그러면 perm 재귀 함수를 통해 문제를 풀어보겠다.

아래 코드를 보면 depth가 M일 경우 출력을 해주는 경우이다.
즉, Base Case 부분이다.
그리고 그 밑에 부분은 중복방지를 위해 check를 이용하여 Recursive Case가 있다. 이렇게 depth와 반복문을 이용하여 문제를 풀었다.
public static void perm(int depth) {
if (depth == m) {
for(int i = 0; i < m; i++) {
System.out.print(output[i] + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
if (!check[i]) {
check[i] = true;
output[depth] = numbers[i];
perm(depth + 1);
check[i] = false;
}
}
}
15655 풀이
이 문제는 기존 15654 문제에서 조건이 하나 더 추가되었다.
고른 수열은 오름차순이어야 한다.
이 조건은 무슨 말이냐면 1 2, 1 3, 1 4는 가능하지만 3 1은 안되는 것이다.
그러면 이전에 작성했던 코드를 이용하여 반복을 할때 i+1번째 수 부터 사용하면 된다.
public static void perm(int depth, int start) {
if (depth == m) {
for(int i = 0; i < m; i++) {
System.out.print(output[i] + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
if (!check[i]) {
check[i] = true;
output[depth] = numbers[i];
perm(depth + 1, i + 1);
check[i] = false;
}
}
}
위의 코드를 보면 start 매개 변수를 받아 재귀할때 i + 1을 하여 오름차순으로 나오게 변경하였다.
15656 풀이
이 문제는 15654 문제에서 같은 수를 여러 번 골라도 된다는 조건이 추가된 문제이다. 즉, 중복을 허용하여 출력해야 한다.
public static void perm(int depth) {
if (depth == m) {
for(int i = 0; i < m; i++) {
System.out.print(output[i] + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
// if (!check[i]) {
// check[i] = true;
output[depth] = numbers[i];
perm(depth + 1);
// check[i] = false;
// }
}
}
위의 코드를 보면 중복 검사를 하는 부분을 모두 주석처리하였다.
하지만 이렇게 제출을 하면 시간 초과가 발생하게 된다.
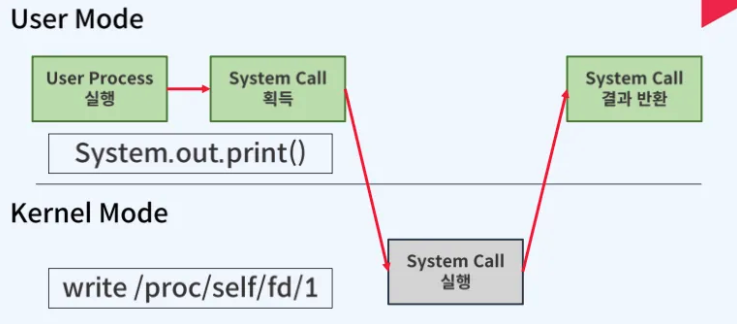

그 이유는 System.out.print()가 n^n회 시스템 콜을호출한다.
그리하여 StringBuilder를 사용하여 출력을 한번에 모아서 출력을 하면 시간초과가 발생하지 않는다.
public static StringBuilder sb = new StringBuilder();
public static void perm(int depth) {
if(depth == M) {
for (int i = 0; i < M; i++)
sb.append(output[i] + " ");
sb.append("\\n");
return;
}
for(int i = 0; i < N; i++) {
// if (!check[i]) {
// check[i] = true;
output[depth] = numbers[i];
perm(depth+1);
// check[i] = false;
// }
}
}
}
15657 풀이
마지막 문제로서 이문제는 같은 수를 여러번 골라도 되고 고른 수열은 오름차순을 만족해야하는 15656과 15655를 동시에 만족하는 문제이다.
그러면 start를 사용하고 check를 사용하지 않게 한다.
그리고 이때는 1 1, 7 7 도 허용하기에 i+1를 start에 넣지 않고 i자체를 넣어주면 된다.
import java.util.*;
class Main {
static int N, M;
static int[] numbers;
// static boolean[] check;
static int[] output;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
M = sc.nextInt();
numbers = new int[N];
// check = new boolean[N];
output = new int[N];
for(int i = 0; i < N; i++)
numbers[i] = sc.nextInt();
Arrays.sort(numbers);
perm(0, 0);
System.out.print(sb);
}
public static StringBuilder sb = new StringBuilder();
public static void perm(int depth, int start) {
if(depth == M) {
for (int i = 0; i < M; i++)
sb.append(output[i] + " ");
sb.append("\\n");
return;
}
for(int i = start; i < N; i++) {
// if (!check[i]) {
// check[i] = true;
output[depth] = numbers[i];
perm(depth+1, i);
// check[i] = false;
// }
}
}
}
'알고리즘 > Recursion' 카테고리의 다른 글
| [코딩테스트] [2529] 부등호 & [9095] 1,2,3 더하기 & [12101] 1,2,3 더하기 2 (1) | 2025.03.25 |
|---|---|
| [코딩테스트] [1759] 암호 만들기 & [10971] 외판원 순회 2 & [14888] 연산자 끼워넣기 (2) | 2025.02.19 |
| [코딩테스트] [1182] 부분수열의 합 & [2758] 로또 & [1208] 부분 수열의 합2 (0) | 2025.02.12 |
| [코딩테스트] [14267] 회사 문화 1 & [1068] 트리 & [5639] 이진 검색 트리 (0) | 2025.02.12 |
| [코딩테스트] [11725] 트리의 부모 찾기 & [1991] 트리 순회 & [15681] 트리와 쿼리 (0) | 2025.02.11 |
