시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 1 초 | 128 MB | 22154 | 6761 | 4625 | 29.061% |
문제
현우는 용돈을 효율적으로 활용하기 위해 계획을 짜기로 하였다. 현우는 앞으로 N일 동안 자신이 사용할 금액을 계산하였고, 돈을 펑펑 쓰지 않기 위해 정확히 M번만 통장에서 돈을 빼서 쓰기로 하였다. 현우는 통장에서 K원을 인출하며, 통장에서 뺀 돈으로 하루를 보낼 수 있으면 그대로 사용하고, 모자라게 되면 남은 금액은 통장에 집어넣고 다시 K원을 인출한다. 다만 현우는 M이라는 숫자를 좋아하기 때문에, 정확히 M번을 맞추기 위해서 남은 금액이 그날 사용할 금액보다 많더라도 남은 금액은 통장에 집어넣고 다시 K원을 인출할 수 있다. 현우는 돈을 아끼기 위해 인출 금액 K를 최소화하기로 하였다. 현우가 필요한 최소 금액 K를 계산하는 프로그램을 작성하시오.
입력
1번째 줄에는 N과 M이 공백으로 주어진다. (1 ≤ N ≤ 100,000, 1 ≤ M ≤ N)
2번째 줄부터 총 N개의 줄에는 현우가 i번째 날에 이용할 금액이 주어진다. (1 ≤ 금액 ≤ 10000)
출력
첫 번째 줄에 현우가 통장에서 인출해야 할 최소 금액 K를 출력한다.
문제풀이
이 문제는 N일 동안 사용할 금액이 먼저 주어진다.
정확히 M번 K원을 인출하여 사용할 때 계획을 만족하는 인출 금액 K의 최소값을 구하는 문제이다.
(주의점: 돈을 인출할 때 남은 돈은 통장에 다시 넣는다.)
예시
아래 이미지에 예시를 하나 만들어보겠다.
그러면 총 두가지의 방법으로 금액을 사용할 수 있다.
그렇다면 900원을 인출한다해도 내가 원하는 순간에 인출을 하여 사용한다면 3번에 맞춰 사용할 수 있다.

하지만 799원을 인출한다고 가정을 하면 총 4번을 인출해야 하는 상황이 나온다.

그렇다면 결론이 나온다.
- 한 번에 k만큼 인출할 때 최소 인출횟수 ≤ M이라면 k는 답이 될 수 있다 그래서 더 적은 금액에 대해 확인해본다.
- 최소 인출횟수 > M이라면 k보다 큰 금액을 인출해야 한다.
자 그러면 문제를 풀어보자.
1. 한 번에 인출할 금액의 탐색 범위를 정하자
이분 탐색 방법을 사용할 것 이기에 탐색 범위를 정해야 한다.
int l = 1, r = N * 10000, ans = -1;
2. 인출 금액에 대해 해당 금액으로 M번 이하로 출금할 수 있다면 인출액을 줄여본다.
2.1 M번 이하로 출금하는게 불가능하다면 인출액을 늘린다.
while (l <= r) {
int m = (l + r) / 2;
if (isPossible(useAmounts, m, M)) {
ans = m;
r = m - 1;
}
else {
l = m + 1;
}
}
3. 조건을 만족하는지 검사하는 함수 작성
현재 상태에서 최적의 해답을 선택하고 조건이 맞는지 찾는 Greedy Algorithm을 이용하자.
static boolean isPossible(int[] useAmounts, int drawAmount, int maxDrawCount) {
int drawCount = 1;
int currentAmount = drawAmount;
for (int useAmount : useAmounts) {
if (useAmount > drawAmount) return false;
if (useAmount > currentAmount) {
if (drawCount == maxDrawCount) return false;
drawCount++;
currentAmount = drawAmount;
}
currentAmount -= useAmount;
}
return true;
}
4. 가능한 인출액 중 최소 금액 출력하기
System.out.println(ans);
전체코드
import java.util.Scanner;
class Main {
static boolean isPossible(int[] useAmounts, int drawAmount, int maxDrawCount) {
int drawCount = 1;
int currentAmount = drawAmount;
for (int useAmount : useAmounts) {
if (useAmount > drawAmount) return false;
if (useAmount > currentAmount) {
if (drawCount == maxDrawCount) return false;
drawCount++;
currentAmount = drawAmount;
}
currentAmount -= useAmount;
}
return true;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int[] useAmounts = new int[N];
for (int i = 0; i < N; i++) {
useAmounts[i] = sc.nextInt();
}
int l = 1, r = N * 10000, ans = -1;
while (l <= r) {
int m = (l + r) / 2;
if (isPossible(useAmounts, m, M)) {
ans = m;
r = m - 1;
}
else {
l = m + 1;
}
}
System.out.println(ans);
}
}
시간복잡도
이 알고리즘의 시간복잡도는 ParametricSearch를 K의 최대값만큼 하여 O(logK)인데 조건을 만족하는지 검사할 때 N번만큼 반복하니 O(N * logK)이다.
[2110] 공유기설치
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 | 128 MB | 83176 | 30349 | 20968 | 36.987% |
문제
도현이의 집 N개가 수직선 위에 있다. 각각의 집의 좌표는 x1, ..., xN이고, 집 여러개가 같은 좌표를 가지는 일은 없다.
도현이는 언제 어디서나 와이파이를 즐기기 위해서 집에 공유기 C개를 설치하려고 한다. 최대한 많은 곳에서 와이파이를 사용하려고 하기 때문에, 한 집에는 공유기를 하나만 설치할 수 있고, 가장 인접한 두 공유기 사이의 거리를 가능한 크게 하여 설치하려고 한다.
C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로 하는 프로그램을 작성하시오.
입력
첫째 줄에 집의 개수 N (2 ≤ N ≤ 200,000)과 공유기의 개수 C (2 ≤ C ≤ N)이 하나 이상의 빈 칸을 사이에 두고 주어진다. 둘째 줄부터 N개의 줄에는 집의 좌표를 나타내는 xi (0 ≤ xi ≤ 1,000,000,000)가 한 줄에 하나씩 주어진다.
출력
첫째 줄에 가장 인접한 두 공유기 사이의 최대 거리를 출력한다.
문제풀이
이 문제를 이해하는데 나는 어려움이 있었다.. 🧐
“가장 인접한 두 공유기 사이의 거리를 가능한 크게 하여 설치하려고 한다.”
위의 말이 “가장 인접한 두 공유기 사이의 최대 거리를 출력한다.”인데.. 나는 도대체 이게 무슨 말 인가 싶다..
예시
예시를 만들어서 이해해보자. 일단 아래 처럼 예시가 주어졌다고 가정해보자.
그러면 총 5개의 집이 있고 4개의 공유기를 설치해야 한 다.
이 때, 공유기의 최대 거리는 2인데 이게 무슨 말인지 한 번 파보자.
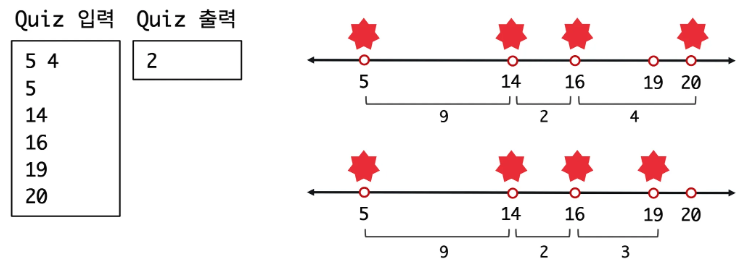
아래 이미지를 예시로 보면 가장 인접한 두 공유기(즉, 14와 16)의 거리는 2이다.
그러면 나머지 거리들도 2 이상이어야 된다. 나머지 거리는 9랑 4이니 만족하는 것.
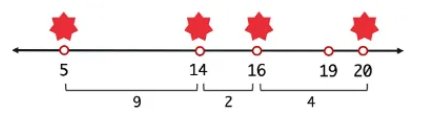
아래 이미지도 보면 가장 인접한 두 공유기 사이의 최대 거리가 2일때 모두 만족한다.
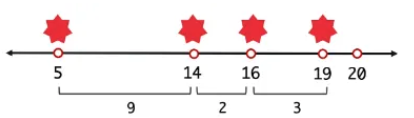
그러면 아래 이미지를 보자. 아래 이미지는 만약 가장 인접한 두 공유기 사이의 최대 거리가 3이라면? 그러면 14와 16번째 집에 공유기를 둘 수 없으니 아래 처럼 공유기를 배치 해야 한 다.
그러면 문제가 발생한다. 20번째 집에도 놓을 수 없고 16번째 집에도 놓을 수 없다. 왜냐하면 두 공유기 사이의 거리가 3이상의 거리를 유지해야 하기 때문이다.
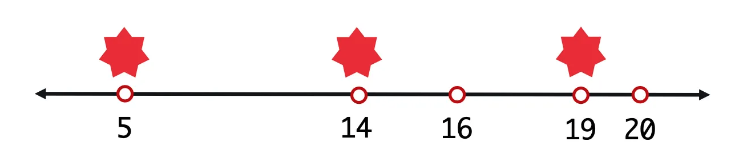
위의 예시들을 보며 아래처럼 결론이 나올 수 있다.
0. 공유기 사이의 거리가 가능한지 구하는 함수
문제
- N개의 집 중 C개의 집을 골라 공유기를 설치할 때 가장 인접한 두 공유기 사이의 최대 거리를 구하라
공유기 사이의 거리를 d이상으로 배치할 때
- C ≤ 배치 가능 개수 라면 D는 답이 될 수 있다.
- C > 배치 가능 개수 라면 공유기 사이 거리를 더 줄여야 한다.
static int calculateCount(int[] xs, int distance) {
int pastX = xs[0];
int cnt = 1;
for(int i = 1; i<xs.length; i++) {
if( xs[i] - pastX >= distance ) {
pastX = xs[i];
cnt++;
}
}
return count;
}
1. 공유기 사이의 거리 탐색 범위를 정하자.
시작 범위와 끝 범위를 정해야 한다.
공유기의 거리를 기준으로 탐색을 하기 때문에 공유기 사이의 최소값과 최대값을 구하자.
그리고 정답을 넣어줄 값도 초기화 해주자.
공유기 사이의 최소값은 1이 될 것 이고 최대값은 제일 마지막 위치값이 될 것이다.
Arrays.sort(xs);
int l = 1, r = xs[N-1], ans = -1;
2. 인접한 공유기 사이의 거리에 대해 배치가 가능하면 정답을 갱신하자.
while(l <= r) {
int m = (l + r)/2;
if(calculateCount(xs, m) >= C) {
ans = m;
l = m + 1;
}
else r = m - 1;
}
3. 정답을 출력하자.
System.out.println(ans);
전체코드
import java.util.Arrays;
import java.util.Scanner;
class Main {
static int calculateCount(int[] xs, int distance) {
int pastX = xs[0];
int cnt = 1;
for(int i = 1; i<xs.length; i++) {
if( xs[i] - pastX >= distance ) {
pastX = xs[i];
cnt++;
}
}
return cnt;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int C = sc.nextInt();
int[] xs = new int[N];
for (int i = 0; i < N; i++) {
xs[i] = sc.nextInt();
}
Arrays.sort(xs);
int l = 1, r = xs[N-1], ans = -1;
while(l <= r) {
int m = (l + r)/2;
if(calculateCount(xs, m) >= C) {
ans = m;
l = m + 1;
}
else r = m - 1;
}
System.out.println(ans);
}
}
시간복잡도
이 알고리즘의 시간 복잡도는 입력받을때 O(N), 공유기 설치 개수를 구할 때 O(n)인데 이분탐색방법을 사용하니 O(Nlogr)이다.
이때 r은 주어진 집의 거리 중 가장 먼 값이다.
'알고리즘 > Binary Search' 카테고리의 다른 글
| [코딩테스트] Parametric Search [2417] 제곱근 구하기 & [2805] 나무자르기 & [1654] 랜선 자르기 (1) | 2024.12.19 |
|---|---|
| [코딩테스트] [2470] 두 용액 & [10816] 숫자 카드 2 (0) | 2024.12.18 |
| [코딩테스트] [2295] 세 수의 합 (0) | 2024.12.17 |
