Parmaetric Search
Binary Search를 이용한 최적값 탐색 기법을 Parmaetric Search라고 한다.
최적값이란, ~~를 할 수 있는 최소값, 최대값, 어떤 조건을 만족하는 최적값을 의미한다. 좀 더 자세히 봐보자.
- 연속적이거나 이산적인 값의 집합에서 최적갑 X를 찾는 문제에서 X를 경계로 조건을 만족하는 집합과 답이 될 수 없는 집합을 판정할 수 있을 때 추정값 A에 대한 판정을 반복해 X를 찾는 방법이다.
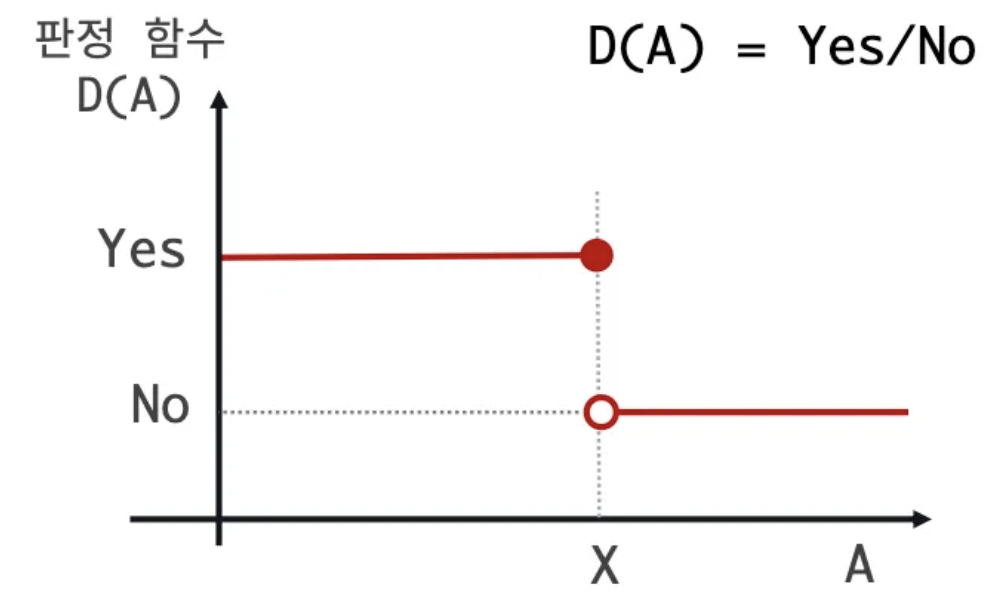
- 이전에 풀었던 문제 숫자 카드 2를 비유해서 봐보자.
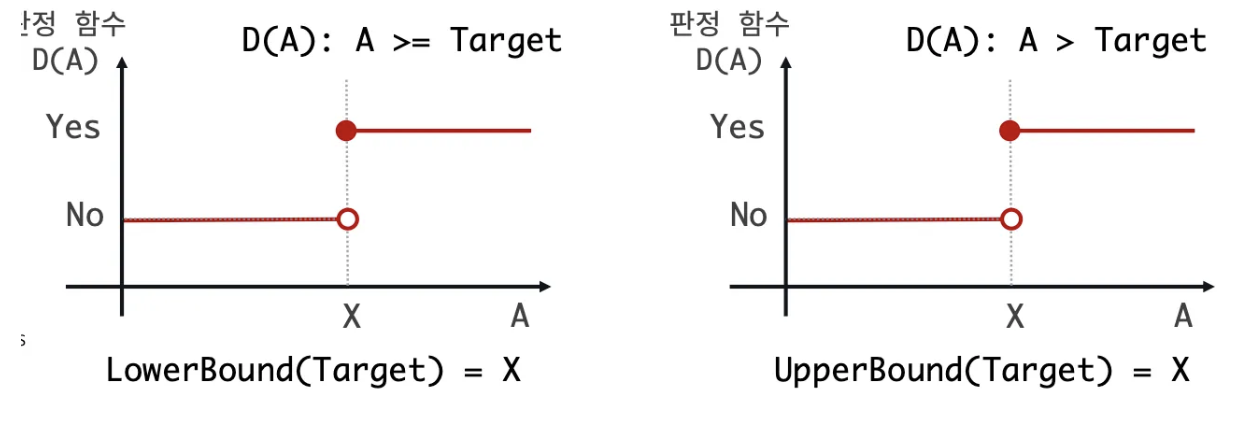
- 모든 추정값 A를 모두 확인하지 않아도 최적값 X를 기준으로 판정결과가 나눠진다면 Binary Search를 적용해볼 수 있다.
- 그렇다면 Parmaetric Search를 이용한 문제를 풀어 보자.
[2417] 정수제곱근
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 0.4 초 (추가 시간 없음) | 128 MB | 17845 | 4194 | 3332 | 27.191% |
문제
정수가 주어지면, 그 수의 정수 제곱근을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 정수 n이 주어진다. (0 ≤ n < 263)
출력
첫째 줄에 q2 ≥ n인 가장 작은 음이 아닌 정수 q를 출력한다.
문제풀이
이 알고리즘은 q2 ≥ n인 가장 작은 음이 아닌 정수 제곱근 q를 구하는 문제이다.
예를 들어서 20이라는 n이 주어졌을때 q가 4일때 16 < 20, 5일때 20<25가 된다.
6,7,8도 만족하지만 가장 작은 값은 5이다.
그래서 위의 알고리즘을 구현하는 코드를 작성해보자.
D(q): q^2 ≥ n;
static boolean isIntegerSqrt(long N, long q) {
rturn q * q >= N;
}
가장 작은 정수를 X라고 할때 X가 True이면 X보다 큰값은 무조건 True가 나온다.
X가 조건을 만족하는 가장 작은 정수이니깐 X보다 작은 값이라면 False가 무조건 나온다.
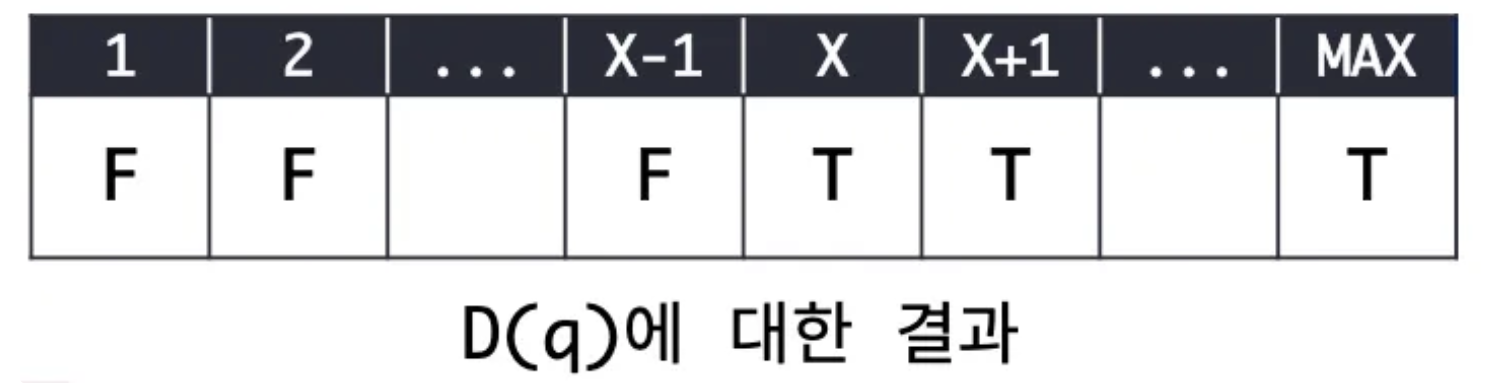
이것을 그래프로 그리면 아래처럼 나오게 된다.

이제 이분 탐색 방법을 하게 된다면 가장 작은 값을 찾을때까지 계속 반복하면 된다.
True가 나오면 왼쪽으로 이동하면 되고 False가 나오면 오른쪽으로 이동하면 된다.
코드로 나타내보자.
n의 범위가 (0 ≤ n < 2^63)이이어서r의 크기를 1L << 32이로 두었냐면 정수 제곱근의 최대 범위까지 넣기 위해서이다.
import java.util.Scanner;
class Main
{
static long calcSqrtInteger(long x) {
if (x == 0) return 0;
long l = 1, r = 1L << 32, sqrt = -1;
while(l <= r) {
long m = (r + l) / 2;
if (m >= (x - 1) / m + 1) {
r = m - 1;
sqrt = m;
}
else l = m + 1;
}
return sqrt;
}
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
long N = sc.nextLong();
System.out.println(calcSqrtInteger(N));
}
}
시간복잡도
이 알고리즘의 시간복잡도는 이분탐색방법만 사용하니 O(logN)이 된다.
[2805] 나무자르기
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 1 초 | 256 MB | 225307 | 67510 | 41871 | 26.611% |
문제
상근이는 나무 M미터가 필요하다. 근처에 나무를 구입할 곳이 모두 망해버렸기 때문에, 정부에 벌목 허가를 요청했다. 정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내주었고, 상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할것이다.
목재절단기는 다음과 같이 동작한다. 먼저, 상근이는 절단기에 높이 H를 지정해야 한다. 높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라간다. 그 다음, 한 줄에 연속해있는 나무를 모두 절단해버린다. 따라서, 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다. 예를 들어, 한 줄에 연속해있는 나무의 높이가 20, 15, 10, 17이라고 하자. 상근이가 높이를 15로 지정했다면, 나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고, 상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다. (총 7미터를 집에 들고 간다) 절단기에 설정할 수 있는 높이는 양의 정수 또는 0이다.
상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가려고 한다. 이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.
출력
적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
문제풀이
이 문제는 M미터 이상의 나무를 가져갈 수 있는 절단기 높이의 최대값을 구하는 문제이다.
어떤 조건을 만족하는 최대값 혹은 최소값이면 Parametric Search를 적용할 수 있는지 확인해보자.
아래 이미지를 봐보자. 내가 가져갈 수 있는 나무의 합이 만족되서 가져갈 수 있다.
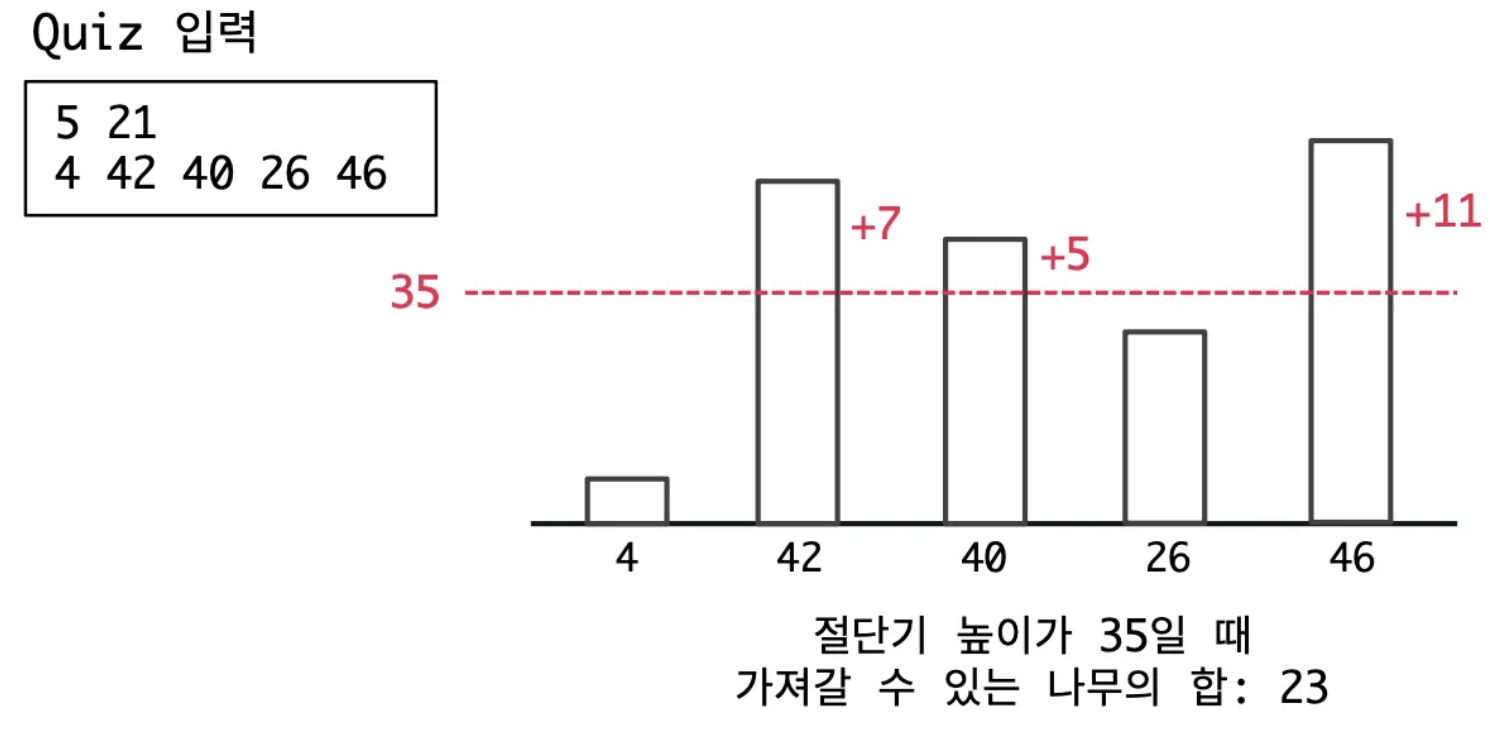
36일때는 가져갈 수 있는 나무의 합이 줄어들어 20이 되기 때문에 36은 안된다.
그러면 35를 기점으로 35보다 줄어든다면 가져가야할 나무의 수보다 크기 때문에 만족을 하고
35 초과가 된다면 가져가야할 나무의 수보다 점점 줄어들기 때문에 모두 만족하지 못할것이다.
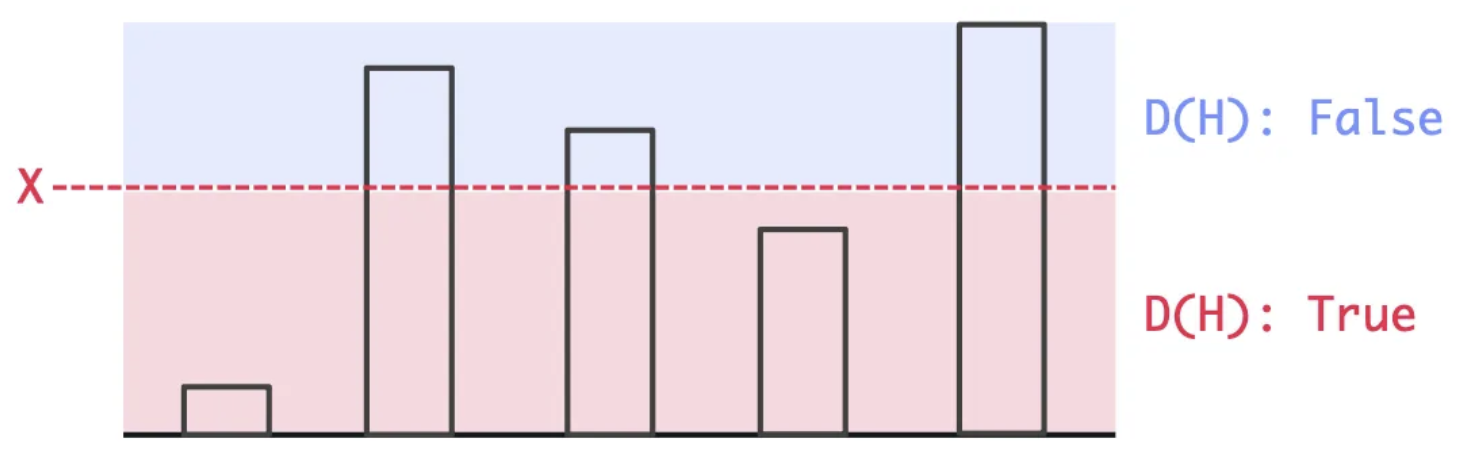
이것을 코드로 변환해보자.
static boolean isPossible(int[] heights, int cutHeight, int thresholdHeight) {
long sum = 0;
for (int h: heights)
if (h > cutHeight) sum += h - cutHeight;
return sum >= thresholdHeight;
}
int l = 0, r = 1000000000, ans = -1;
while (l <= r) {
int m = (l + r ) / 2;
if (isPossibe(h, m, M)) {
ans = m;
l = m + 1;
}
else r = m - 1;
}
1. 절단기 높이의 탐색 범위를 정하자
절단기 높이의 최소값부터 최대값을 지정하자.
그리고 무조건 나무를 자르러 가니 값이 안들어오는 경우가 없기에 ans를 -1로 지정한다.
int l = 0, r = 1000000000, ans = -1;
2.1 원하는 만큼 나무를 가져갈 수 있다며 높이를 높이자
2.2 원하는 만큼 가져갈 수 없다면 높이를 낮추자.
만약 가져가야할 나무 수 M이사이면 ans를 M으로 넣어주자.
반복을 하며 가장 가져갈 수 있는 최대의 값이 들어오게 된다.
while (l <= r) {
// 2. 임의 절단기 높이에 대해
// 2.1 원하는 만큼 나무를 가져갈 수 있다며 높이를 높이자
// 2.2 원하는 만큼 가져갈 수 없다면 높이를 낮추자.
int m = (l + r) / 2;
if ( isPossinble(h, m, M)) {
ans = m;
l = m + 1;
}
else r = m - 1;
}
static boolean isPossinble(int[] height,int cutH, int M) {
long sum = 0;
for (int h: height) {
if (h > cutH) sum += h - cutH;
}
return sum >= M;
}
전체코드
import java.util.Scanner;
class Main {
static boolean isPossinble(int[] height,int cutH, int M) {
long sum = 0;
for (int h: height) {
if (h > cutH) sum += h - cutH;
}
return sum >= M;
}
public static void main (String[] args) {
// 0. 입력 받기
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int[] h = new int[N];
for (int i = 0; i<N; i++)
h[i] = sc.nextInt();
// 1. 절단기 높이의 탐색 범위를 정한다.
int l = 0, r = 1000000000, ans = -1;
while (l <= r) {
// 2. 임의 절단기 높이에 대해
// 2.1 원하는 만큼 나무를 가져갈 수 있다며 높이를 높이자
// 2.2 원하는 만큼 가져갈 수 없다면 높이를 낮추자.
int m = (l + r) / 2;
if ( isPossinble(h, m, M)) {
ans = m;
l = m + 1;
}
else r = m - 1;
}
System.out.println(ans);
}
}
시간복잡도
이 알고리즘의 시간복잡도는 N번만큼 반복하기에 O(N) * H만큼 이분탐색방법을 하기에 (logH) 즉, O(NlogH)이다.
[1654] 랜선 자르기 성공
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 | 128 MB | 250689 | 60245 | 40732 | 21.649% |
문제
집에서 시간을 보내던 오영식은 박성원의 부름을 받고 급히 달려왔다. 박성원이 캠프 때 쓸 N개의 랜선을 만들어야 하는데 너무 바빠서 영식이에게 도움을 청했다.
이미 오영식은 자체적으로 K개의 랜선을 가지고 있다. 그러나 K개의 랜선은 길이가 제각각이다. 박성원은 랜선을 모두 N개의 같은 길이의 랜선으로 만들고 싶었기 때문에 K개의 랜선을 잘라서 만들어야 한다. 예를 들어 300cm 짜리 랜선에서 140cm 짜리 랜선을 두 개 잘라내면 20cm는 버려야 한다. (이미 자른 랜선은 붙일 수 없다.)
편의를 위해 랜선을 자르거나 만들 때 손실되는 길이는 없다고 가정하며, 기존의 K개의 랜선으로 N개의 랜선을 만들 수 없는 경우는 없다고 가정하자. 그리고 자를 때는 항상 센티미터 단위로 정수길이만큼 자른다고 가정하자. N개보다 많이 만드는 것도 N개를 만드는 것에 포함된다. 이때 만들 수 있는 최대 랜선의 길이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그 후 K줄에 걸쳐 이미 가지고 있는 각 랜선의 길이가 센티미터 단위의 정수로 입력된다. 랜선의 길이는 231-1보다 작거나 같은 자연수이다.
출력
첫째 줄에 N개를 만들 수 있는 랜선의 최대 길이를 센티미터 단위의 정수로 출력한다.
문제풀이
이 문제는 길이가 제각각인 K개의 랜선으로 N개의 같은 길이의 랜선으로 만들 때 만들 수 있는 최대 랜선의 길이를 구하는 문제이다
만약 길이 X의 래선을 만들 수 있는 개수가 K라면
- k < N이라면 랜선 길이를 줄여야한다
- k >= N이라면 X는 답이될 수 있고 더 긴 길이의 랜선을 만들어본다
즉, X가 길수록 k가 작아지므로 답이 될 수 없고, X가 짧을수록 k가 커지므로 답이 될 수 있다.
static int calculate(int[] len, long cutLength) {
int cnt = 0;
for (int l: len) {
cnt += l / cutLength;
}
return cnt;
}
1. 만들어볼 랜선 길이의 탐색 범위 정하기
r은 랜선의 길이로 랜선의 길이는 2^31-1보다 작거나 같은 자연수이다.
long l = 1, r = (1L << 32) - 1, ans = -1;
2. 임의 래선 길이에 해당 길이 랜선을 N개 이상 만들 수 있다면 길이를 늘린다.
2.1 N개 이상 만들 수 없다면 길이를 줄여본다.
Parametric Search를 사용하여 N개 이상의 개수를 가질 수 있을때 ans를 계속 업데이트 해주자.
만약 랜선을 N개 이상 만들 수 있다면 길이를 늘리기 때문에 l = m + 1;
N개 이상 만들 수 없다면 길이를 줄여본다. r = m - 1;
while(l <= r ) {
long m = (l + r) / 2;
if(calculate(len, m) >= N) {
ans = m;
l = m + 1;
}
else r = m - 1;
}
// 몇개를 가질 수 있는지 계산하는 함수
static int calculate(int[] len, long cutLength) {
int cnt = 0;
for (int l: len) {
cnt += l / cutLength;
}
return cnt;
}
3. N개 이상 만들 수 있었던 길이 중 최댓값을 출력한다.
System.out.println(ans);
전체코드
import java.util.Scanner;
class Main {
static int calculate(int[] len, long cutLength) {
int cnt = 0;
for (int l: len) {
cnt += l / cutLength;
}
return cnt;
}
public static void main (String[] args) {
// 0. 입력 받기
Scanner sc = new Scanner(System.in);
int K = sc.nextInt();
int N = sc.nextInt();
int[] len = new int[K];
for (int i = 0; i<K; i++)
len[i] = sc.nextInt();
long l = 1, r = (1L << 32) - 1, ans = -1;
while(l <= r ) {
long m = (l + r) / 2;
if(calculate(len, m) >= N) {
ans = m;
l = m + 1;
}
else r = m - 1;
}
System.out.println(ans);
}
}
시간복잡도
이 알고리즘의 시간복잡도는 입력할 때 O(K), 랜선의 길이가 N개 이상인 지 구하는 방법(logr)
즉, O(Klogr)이다.
'알고리즘 > Binary Search' 카테고리의 다른 글
| [코딩테스트] [6236] 용돈관리 & [2110] 공유기설치 (0) | 2024.12.23 |
|---|---|
| [코딩테스트] [2470] 두 용액 & [10816] 숫자 카드 2 (0) | 2024.12.18 |
| [코딩테스트] [2295] 세 수의 합 (0) | 2024.12.17 |
