[17232] 생명 게임
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 | 512 MB | 785 | 284 | 224 | 46.186% |
문제
생명 게임은 수학자 콘웨이(John Horton Conway)가 창안한 게임으로, 바둑판 모양의 격자에 '생명'을 배치하고 그 변화를 관찰하는 게임이다.

준표는 콘웨이가 창안한 생명 게임에서 사소한 조건을 바꿔 새로운 규칙의 생명 게임을 제안 해보았다.
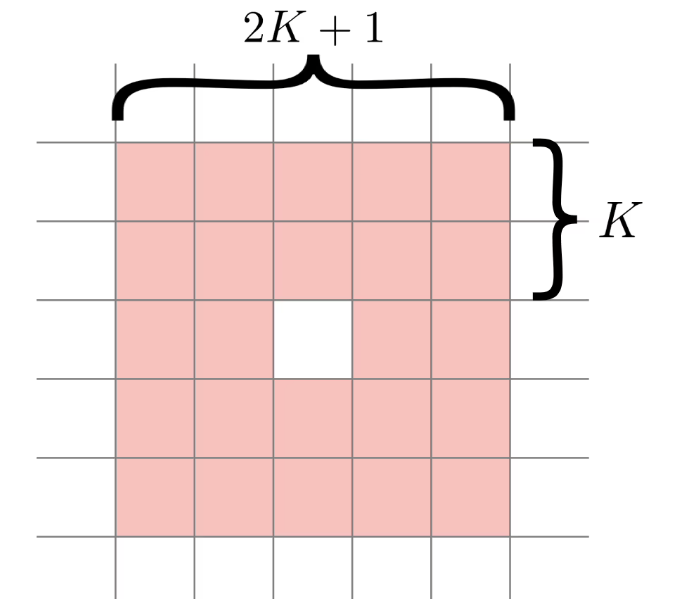
바둑판의 각 칸은 주위에 몇 개의 생명이 존재하는지에 따라 다음 상황이 아래와 같이 결정된다.
- 생존 : 만약 현재 칸에 생명이 있고, 주위에 a개 이상 b개 이하의 생명이 있다면 현재 칸의 생명은 다음 단계에 살아남는다.
- 고독 : 만약 현재 칸에 생명이 있고, 주위에 a개 미만의 생명이 있다면 현재 칸의 생명은 외로워서 죽는다.
- 과밀 : 만약 현재 칸에 생명이 있고, 주위에 b개 초과의 생명이 있다면 현재 칸의 생명은 과밀로 죽는다.
- 탄생 : 만약 현재 칸에 생명이 없고, 주위에 a개 초과 b개 이하의 생명이 있다면 다음 단계에서 현재 칸에 생명이 생긴다.
생명은 바둑판을 벗어난 영역에서는 생존할 수 없다.
준표는 N×M 크기의 바둑판에 생명을 뿌리고, T시간 뒤의 생명을 관찰하고자 한다.
입력
첫줄에는 바둑판의 세로길이, 가로길이를 나타내는 두 정수 N과 M, 준표가 바둑판을 관찰하고자 하는 시간 T가 주어진다.
두번째 줄에는 주위의 기준이 되는 정수 K, 각 칸의 다음 상황을 결정하는 정수 a, b가 주어진다.
다음 N개의 줄에 걸쳐 바둑판의 처음 상태가 주어진다. 각 줄은 길이 M의 문자열로 생명이 있는 칸은 '*', 빈칸은 '.'로 주어진다.
출력
N개의 줄에 걸쳐 바둑판의 상태를 출력한다. 각 줄은 길이 M의 문자열로 생명이 있는 칸은 '*', 빈칸은 '.'로 출력한다.
제한
- 1 ≤ N, M ≤ 100
- 1 ≤ T ≤ 300
- 0 ≤ a, b < (2×K+1)
- 2
서브태스크 1 (100점)
- K = 1
서브태스크 2 (40점)
- 1 ≤ K ≤ max(N, M)
문제풀이
이 문제는 N*M 바둑판에서 1시간마다 각 칸을 중심으로 주위 (2K+1) * (2K+1) 생명에 따라 아래 상황이 발생할 때, T시간 뒤 생명현황을 찾는 문제이다.
- 생존: 현재 칸에 생명이 있고, a ≤ 주위 생명 ≤ b 라면 해당 칸의 생명은 생존
- 고독: 현재 칸에 생명이 있고, 주위생명 ≤ a라면 해당 칸의 생명은 외로워서 죽음
- 과밀: 현재 칸에 생명이 있고, b < 주위생명이라면 해당 칸의 생명은 과밀로 죽는다.
- 탄생: 현재 칸에 생명이 없고, a < 주위생명 ≤ b 라면 해당 칸에 생명이 생긴다.
0. 입력받기
우리는 편한 비교를 위해 1부터 사용하기 위해 N+1, M+1 이차원 배열을 만들어 주자.
// 0. 입력받기
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int T = sc.nextInt();
int K = sc.nextInt();
int A = sc.nextInt();
int B = sc.nextInt();
char[][] map = new char[N+1][M+1];
for(int i=1; i<=N; i++) {
String rowMap = sc.next();
for (int j = 1; j <= M; j++) {
map[i][j] = rowMap.charAt(j-1);
}
}
1. 현재 칸의 주변을 파악해보자.
2K+1 즉, 주위에 생명이 얼마나 있는지 파악해여 현재 칸의 상태가 어떻게 변화할 지 알 수 있다.
매번 (2K+1)*(2K+1) 범위를 다 확인한다면?
static int getRange(char[][] map, int r, int c, int K) {
int sum = 0;
for (int i = Math.max(r - K, 0); i <= Math.min(r + K, map.length - 1); i++)
for (int j = Math.max(c - K, 0); j <= Math.min(c + K, map[0].length - 1); j++)
if (map[i][j] == '*') sum ++;
return sum;
}
2. 조건 충족 위에서 정리한 4가지의 조건을 비교해서 업데이트 해주자.
현재 칸에 대한 생명 여부와 그 주변의 값을 비교하는 알고리즘을 작성했다.
nearAlive < A or B < nearAlive 라면 고독사 혹은 과밀사가 진행된다.
그리고 *이 아닌 경우 주변에 탄생 조건 A < nearAlive && nearAlive <= B을 만족하면 *이 탄생 된다.
while (T-- > 0) {
char[][] nextMap = new char[N + 1][M + 1]; // 다음 상태를 저장할 배열
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
int nearAlive = getRange(map, i, j, K);
if (map[i][j] == '*') {
nearAlive--;
if (nearAlive < A || B < nearAlive)
nextMap[i][j] = '.'; // 고독사 Or 과밀사
else
nextMap[i][j] = '*'; // 생존
} else if (A < nearAlive && nearAlive <= B) {
nextMap[i][j] = '*'; // 탄생
} else {
nextMap[i][j] = '.'; // 빈칸 유지
}
}
}
map = nextMap; // 현재 상태를 다음 상태로 업데이트
}
3. 출력하기
이제 모든 주변 조건을 비교하여 map을 업데이트 하였으니 한줄식 출력하면 된다.
for(int i=1; i<=N; i++) {
for (int j = 1; j <= M; j++)
System.out.print(map[i][j]);
System.out.println();
}
자 이제 예제 1 입력을 입력하면 알맞은 출력 결과가 나오니 한 번 백준에 재출해보자.

그러면 시간복잡도가 O(T * N *M * getRangeSum)이 되면서 시간 복잡도가 초과한다.. 😫
위 알고리즘은 전체를 하나하나씩 비교하여 실행이 되니 시간 효율이 좋지 않다.
그러면 다른 방법으로 풀이해보자.
누적합을 이용한 풀이
생명이 있는 칸을 1, 아닌 칸을 0으로 시간마다 누적합을 구해두고 사용해보자.
static int getRangeSum(int[][] acc, int r, int c, int K) {
int r1 = Math.max(r - K, 1);
int c1 = Math.max(c - K, 1);
int r2 = Math.min(r + K, acc.length - 1);
int c2 = Math.min(c + K, acc[0].length - 1);
return acc[r2][c2] - acc[r1 -1][c2] - acc[r2][c1-1] + acc[r1-1][c1-1];
}
매 시간마다 현재 생명에 대한 누적합 계산이 필요하다.
static int[][] getPrefixSum(char[][] map) {
int[][] acc = new int[map.length][map[0].length];
for(int i=1; i<=map.length-1; i++)
for (int j = 1; j <= map[0].length-1; j++) {
int alive = (map[i][j] == '*' ? 1 : 0);
acc[i][j] = acc[i - 1][j] + acc[i][j - 1] - acc[i - 1][j - 1] + alive;
}
return acc;
}
이 때 시간복잡도는 O(T * (getPrefixSum + N*M * getRangeSum)) ⇒ O(T * N * M)
나머지 코드는 동일하다.
import java.util.Scanner;
class Main
{
static int[][] getPrefixSum(char[][] map) {
int[][] acc = new int[map.length][map[0].length];
for(int i=1; i<=map.length-1; i++)
for (int j = 1; j <= map[0].length-1; j++) {
int alive = (map[i][j] == '*' ? 1 : 0);
acc[i][j] = acc[i - 1][j] + acc[i][j - 1] - acc[i - 1][j - 1] + alive;
}
return acc;
}
static int getRangeSum(int[][] acc, int r, int c, int K) {
int r1 = Math.max(r - K, 1);
int c1 = Math.max(c - K, 1);
int r2 = Math.min(r + K, acc.length - 1);
int c2 = Math.min(c + K, acc[0].length - 1);
return acc[r2][c2] - acc[r1 -1][c2] - acc[r2][c1-1] + acc[r1-1][c1-1];
}
public static void main (String[] args) {
// 0. 입력받기
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int T = sc.nextInt();
int K = sc.nextInt();
int A = sc.nextInt();
int B = sc.nextInt();
char[][] map = new char[N+1][M+1];
for(int i=1; i<=N; i++) {
String rowMap = sc.next();
for (int j = 1; j <= M; j++) {
map[i][j] = rowMap.charAt(j-1);
}
}
while (T-- > 0) {
int[][] acc = getPrefixSum(map);
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
int nearAlive = getRangeSum(acc, i, j, K);
if (map[i][j] == '*') {
nearAlive--;
if (nearAlive < A || B < nearAlive)
map[i][j] = '.';
} else if (A < nearAlive && nearAlive <= B) {
map[i][j] = '*'; // 탄생
}
}
}
}
for(int i=1; i<=N; i++) {
for (int j = 1; j <= M; j++)
System.out.print(map[i][j]);
System.out.println();
}
}
}

이분 탐색(Binary Search)
코딩테스트에서 이분탐색문제는 빈출 문제이고 많은 유형들이 있다.
그래서 이분탐색의 개념과 유형에 대해 학습한다.
정렬되어 있는 집합에서 원하는 값을 찾는 방법
정렬되어 있는 집합에서 원하는 값을 찾는 효율적인 탐색 방법이 있다. 예시를 보자
1. 순차탐색방법
제일 쉬운 방법은 모든 요소를 검사하여 그 값이 있는지 확인하는 방법이다.
boolean isExist(int[] arr, int x) {
for(int a: arr)
if(a == x) return true;
return false;
}
하지만 위의 방법의 시간복잡도를 계산하면 O(N)이다.
만약 20억개의 요소를 탐색한다면 20억번 반복해야 한다는 것이다.
2. 이분탐색방법
그렇다면 정렬되어 있는 집합이란 것을 이용하여 풀어보자.
답이 될 수 있는 범위 [l:r]중 임의의 값 am에 대해 am과 찾는 값 x의 대소 관계에 따라 범위를 좁혀 나가보자.
boolean isExist(int[] arr, int x) {
int l = 0, r = arr.length-1;
while(l <= r) {
int m = (1+r)/2;
if(arr[m] < x)
l = m + 1;
else if(arr[m] > x)
r = m - 1;
else return true;
}
return false;
}
위의 방법의 시간복잡도는 O(logN)이다.
처음 탐색 범위 : N
두 번째 탐색 범위: N / 2
세 번째 탐색 범위: N / 2^2
logN 번째 탐색 범위: N / 2logN
[1920] 수 찾기
그렇다면 문제 하나를 풀어 살펴보자.
문제풀이
이 문제는 N개의 정수가 주어질 때 이 안에 M개의 정수 X가 존재하는지 판단하는 문제이다.
1. 각 숫자가 존재하는지 boolean[] 기록
아래 코드를 사용해서 하면 시간초과가 발생한다.
import java.util.Scanner;
class Main {
static boolean isExist(int[] arr, int x) {
for (int a : arr)
if (a == x) return true;
return false;
}
public static void main(String[] args) {
// 0. 입력받기
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] arr = new int[N+1];
for (int i = 1; i <= N; i++)
arr[i] = sc.nextInt();
int M = sc.nextInt();
// 각 요소에 대해 존재 여부 확인
while(M-->0) {
int m = sc.nextInt();
if (isExist(arr, m)) {
System.out.println(1); // 존재하면 1 출력
} else {
System.out.println(0); // 존재하지 않으면 0 출력
}
}
}
}
2. Set을 사용해 숫자 기록
Set을 사용하여 문제를 풀 수 있다.
set에 x값이 있따면 1를 출력하고 없다면 0을 출력하면 된다.
import java.util.*;
class Main {
public static void main(String[] args) {
// 0. 입력받기
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
Set<Integer> set = new HashSet<>();
for (int i=0; i<N; i++)
set.add(sc.nextInt());
int M = sc.nextInt();
while(M-->0) {
int x = sc.nextInt();
System.out.println(set.contains(x) ? 1 : 0);
}
}
}
3. 주어진 숫자를 정렬해 Binary Seacrh를 사용하여 풀이
Arrys를 정렬하고
binarySearch를 사용하여 0보다 같거나 크다면 1이다.
import java.util.*;
class Main {
public static void main(String[] args) {
// 0. 입력받기
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] arr = new int[N];
for (int i=0; i<N; i++)
arr[i] = sc.nextInt();
Arrays.sort(arr);
int M = sc.nextInt();
while(M-->0) {
int x = sc.nextInt();
int idx = Arrays.binarySearch(arr, x);
System.out.println(idx >= 0 ? 1 : 0);
}
}
}
정리
정렬되어 있는 집합에서 원하는 값을 찾는 효율적인 탐색 방법
집합 전체를 확인하는 O(N)복잡도가 아닌 O(logN)의 복잡도로 탐색 할 수 있다.
- 원하는 값이 존재할 수 있는 범위를 초기화한다.
- 일반적으로 집합의 전체 범위가 첫 조사범위가 된다.
- 현재 유효한 범위의 중앙값과 찾는 값을 비교하여 조사 범위를 좁힌다.
- 중앙값과 같다면 해당 값을 찾았으므로 알고리즘 종료
- 중앙값이 값보다 작다면 조사 범위를 중앙값 이후 범위로 좁힌다.
- 중앙값이 값보다 크다면 조사 범위를 중앙값 이전 범위로 좁힌다.
- 유효범위가 남지 않을때까지 찾지 못하면, 해당 값은 존재하지 않는다.
[14425] 문자열 집합
문자열 집합
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 (하단 참고) | 1536 MB | 61049 | 33137 | 25376 | 53.972% |
문제
총 N개의 문자열로 이루어진 집합 S가 주어진다.
입력으로 주어지는 M개의 문자열 중에서 집합 S에 포함되어 있는 것이 총 몇 개인지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 문자열의 개수 N과 M (1 ≤ N ≤ 10,000, 1 ≤ M ≤ 10,000)이 주어진다.
다음 N개의 줄에는 집합 S에 포함되어 있는 문자열들이 주어진다.
다음 M개의 줄에는 검사해야 하는 문자열들이 주어진다.
입력으로 주어지는 문자열은 알파벳 소문자로만 이루어져 있으며, 길이는 500을 넘지 않는다. 집합 S에 같은 문자열이 여러 번 주어지는 경우는 없다.
출력
첫째 줄에 M개의 문자열 중에 총 몇 개가 집합 S에 포함되어 있는지 출력한다
문제풀이
이 문제도 [1920] 수 찾기 문제처럼 풀면 되는 간단한 문제이다.
Array를 정렬 후 이분탐색방법을 사용하여 풀면 되는 문제이다.
0. 입력 받기
N번 입력후 M번 입력을 해야 한다.
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
String[] arr = new String[N];
for (int i=0; i<N; i++)
arr[i] = sc.next();
// 생략
while(M-->0) {
String x = sc.next();
// 생략
}
1. 정렬 후 이분탐색
이분탐색을 하기 위해 정렬을 하고 Arrays의 메서드인 binarySearch를 하자.
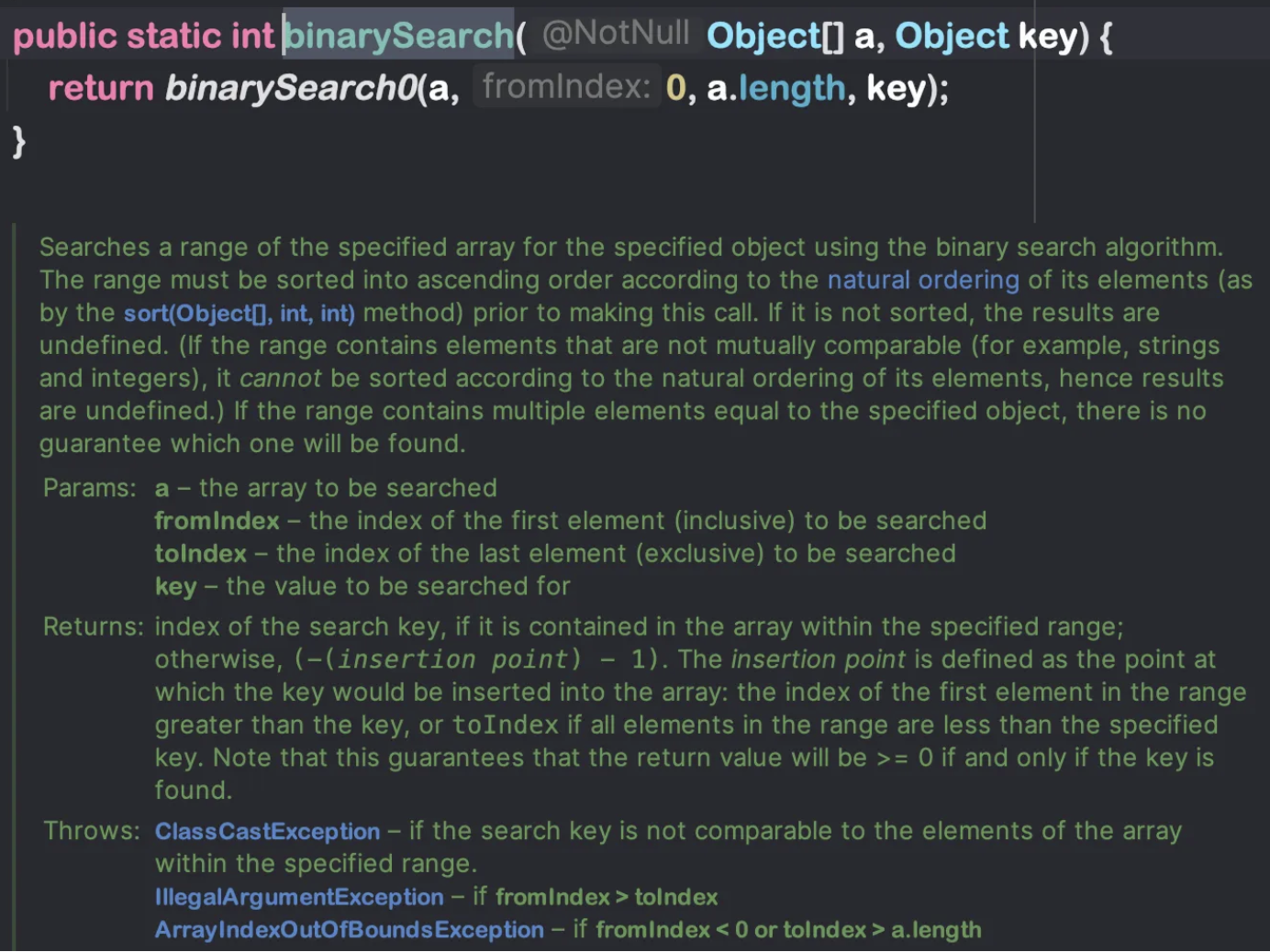
binarySearch는 object 배열 a와 Object key를 받는다. 반환은 검색 키가 배열에 존재하면 해당 키의 인덱스 키가 존재하지 않으면, 삽입 위치를 나타내는 음수 값을 반환한다.
이 값은 -(insertion point) - 1 형식이다.
삽입 위치는 키보다 큰 첫 번째 요소의 인덱스 또는 모든 요소가 키보다 작을 경우 toIndex이다.
count를 만들어주고 idx값이 0과 같고 크다면 값이 포함되는 것이니 count를 1증가 시켜주면 된다!
int count = 0;
while(M-->0) {
String x = sc.next();
int idx = Arrays.binarySearch(arr, x);
if (idx >=0 ) {
count++;
}
}
System.out.println(count);
import java.util.*;
class Main {
public static void main(String[] args) {
// 0. 입력받기
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
String[] arr = new String[N];
for (int i=0; i<N; i++)
arr[i] = sc.next();
Arrays.sort(arr);
int count = 0;
while(M-->0) {
String x = sc.next();
int idx = Arrays.binarySearch(arr, x);
if (idx >=0 ) {
count++;
}
}
System.out.println(count);
}
}
'알고리즘 > Prefix Sum' 카테고리의 다른 글
| [11660] 구간 합 구하기 5 & [19951] 태상이의 훈련소 (0) | 2024.12.13 |
|---|---|
| [코딩테스트] [11659] 구간 합 구하기 4 & [16713] Generic Queries (0) | 2024.12.12 |
