[코딩테스트] [11659] 구간 합 구하기 4 & [16713] Generic Queries

[11659] 구간 합 구하기 4

누적합 배열이 어떻게 사용되는지 문제를 풀어보며 이해해보자.

시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율

1 초

256 MB

138676

56789

41470

38.443%

문제

수 N개가 주어졌을 때, i번째 수부터 j번째 수까지 합을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j가 주어진다.

출력

총 M개의 줄에 입력으로 주어진 i번째 수부터 j번째 수까지 합을 출력한다.

제한

• 1 ≤ N ≤ 100,000
• 1 ≤ M ≤ 100,000
• 1 ≤ i ≤ j ≤ N

문제풀이

이 문제는 수 N개가 주어 졌을 때, M번의 (i, j) 질문에 대해 i번째 수부터 j번째 수까지 합을 구하는 문제이다.

예제 1번의 입출력을 보면 아래처럼 배열의 합이 구해지는 것을 확인할 수 있다.

제일 쉽게 문제를 해결하는 방법은?

바로 각 질문에 대해 매번 [i:j]를 순회해서 답을 구하면 문제에 대한 답은 구할 수 있다!

다만… 시간초과가 발생하는 것만 빼면 말이다.. 😡  순회하여 답을 구하는 코드를 보자.

while (M-->0) {
	int num1 = sc.nextInt();
	int num2 = sc.nextInt();
	
	for (int i=num1; i<=num2; i++)
		sum += arr[i];
		
	System.out.println(sum);
}

위의 코드를 보면 O(M*N)이기 때문에 시간복잡도가 O(N^2)이다. M과 N은 100,000이다.

그래서 다른 해결 방법, 누적합 배열

누적합 배열: acc[i] = Sum(arr[1], arr[i])

아래 이미지를 보면 기존 배열을 하나하나씩 더해서 누적합 acc배열에 추가하는 것이다.

// 방법 1
int sum = 0;
for (int i=1; i<=N; i++) {
	sum+=arr[i];
	acc[i] = sum;
}
// 방법 2
for (int i=1; i<=N; i++)
	acc[i] = acc[i-1] + arr[i];
 

 

그렇다면 누적합을 이용해서 어떻게 구간합을 구하면 될까?

예를 들어 [3:6], 배열의 3번째 인덱스에서 6번째 인덱스까지의 합을 구하기로 해보자.

아래 이미지를 보면 이해가 더 쉬울거다.

위의 그림을 코드로 작성해보겠다.

// l이 시작(3), r이 끝(6)
(acc[r] - acc[l-1]

시간복잡도

이렇게 하면 시간초과가 나지 않고 문제를 맞출 수 있다.

과연 시간복잡도는 어떻게 될까?

누적합 배열을 만들 때 반복문 한 번을 사용하니깐 시간복잡도 O(N)

그리고 구간합을 계산하는 부분에서 시간복잡도 Query의 개수에 만큼 반복되니 O(M)

결론 O(N+M)이다.

        // 1. 누적합배열 만들기
        int[] acc = new int[N+1];
        for(int i=1; i<=N; i++)
            acc[i] = acc[i-1] + arr[i];

전체 코드

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        // 0. 입력받기
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int M = sc.nextInt();
        
        // 1-base로 시작
        int[] arr = new int[N+1];
        for(int i=1; i<=N; i++)
            arr[i] = sc.nextInt();
        
        // 1. 누적합배열 만들기
        int[] acc = new int[N+1];
        for(int i=1; i<=N; i++)
            acc[i] = acc[i-1] + arr[i];

        // l~r까지 합 구하기
        while(M-->0) {
            int l = sc.nextInt();
            int r = sc.nextInt();
            System.out.println(acc[r] - acc[l-1]);
        }
    }
}

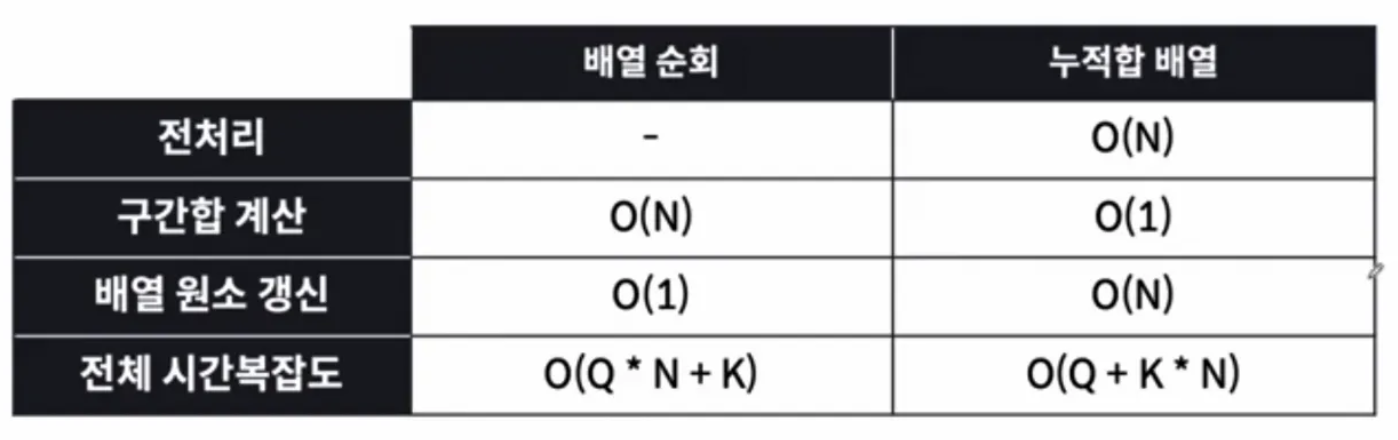
누적합 배열과 배열 순회의 시간복잡도 차이

누적합 배열을 사용시 원본 배열의 원소가 업데이트 된다면 다시 누적합 배열을 계산하여 만들어야 한다.

따라서 배열 원소 갱신 횟수(k)가 크다면 누적합 배열을 사용하더라도 시간복잡도가 개선되지 않을 수 있다!

[16713] Generic Queries

시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율

2.5 초

512 MB

1354

822

652

58.580%

문제

입력

출력

모든 쿼리의 답을 XOR한 값을 출력하시오.

문제풀이

이 문제는 이전 문제 [11659] 구간 합 구하기 4과 같은 유형의 문제이다.

누적합 배열을 사용해서 구간합을 구하면 되는 문제이다.

다만 다른 점이 있는데 이전 문제에서는 합을 구하는 문제였다면 지금 문제에서는 XOR를 구하면 되는 문제이다.

즉, 구간XOR을 구하고 구한 답들(Query의 개수)끼리 다시 XOR 계산을 해주면 되는 문제이다.

그러면 XOR 연산이 무엇인지 알아보자.

XOR 계산 방법

OR은 x, y값중 하나라도 1이 존재하면 1을 반환해준다.

XOR은 1이 하나만 있을 때 1을 반환해준다, 모두 1이면 0을 반환한다.

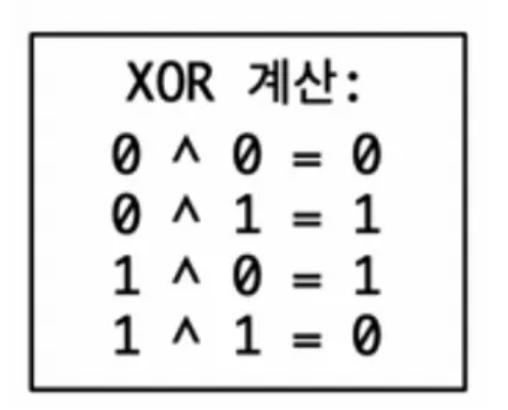
그러면 어떻게 계산을 해줘야할까? 바로 이진수변환을 이용하면 된다! 😙

arr[]은 아래처럼 값을 갖고 있다. 이것을 이진수 변환을 하여 XOR 계산을 진행할것이다.

 

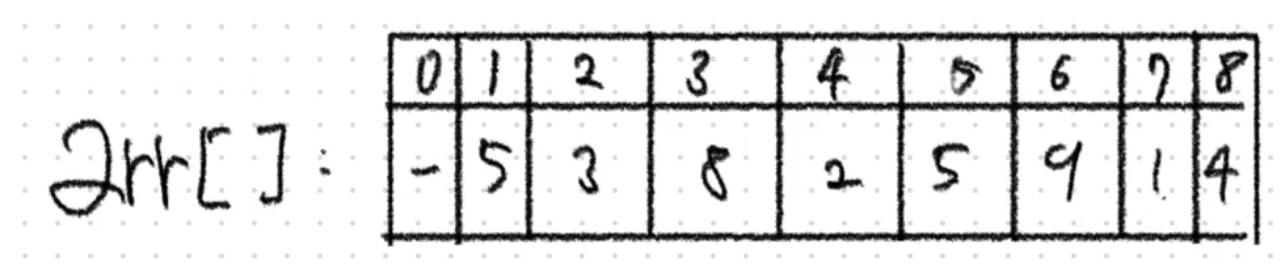
1번째 원소에서 5번째 원소까지 XOR한 값을 구해보자.

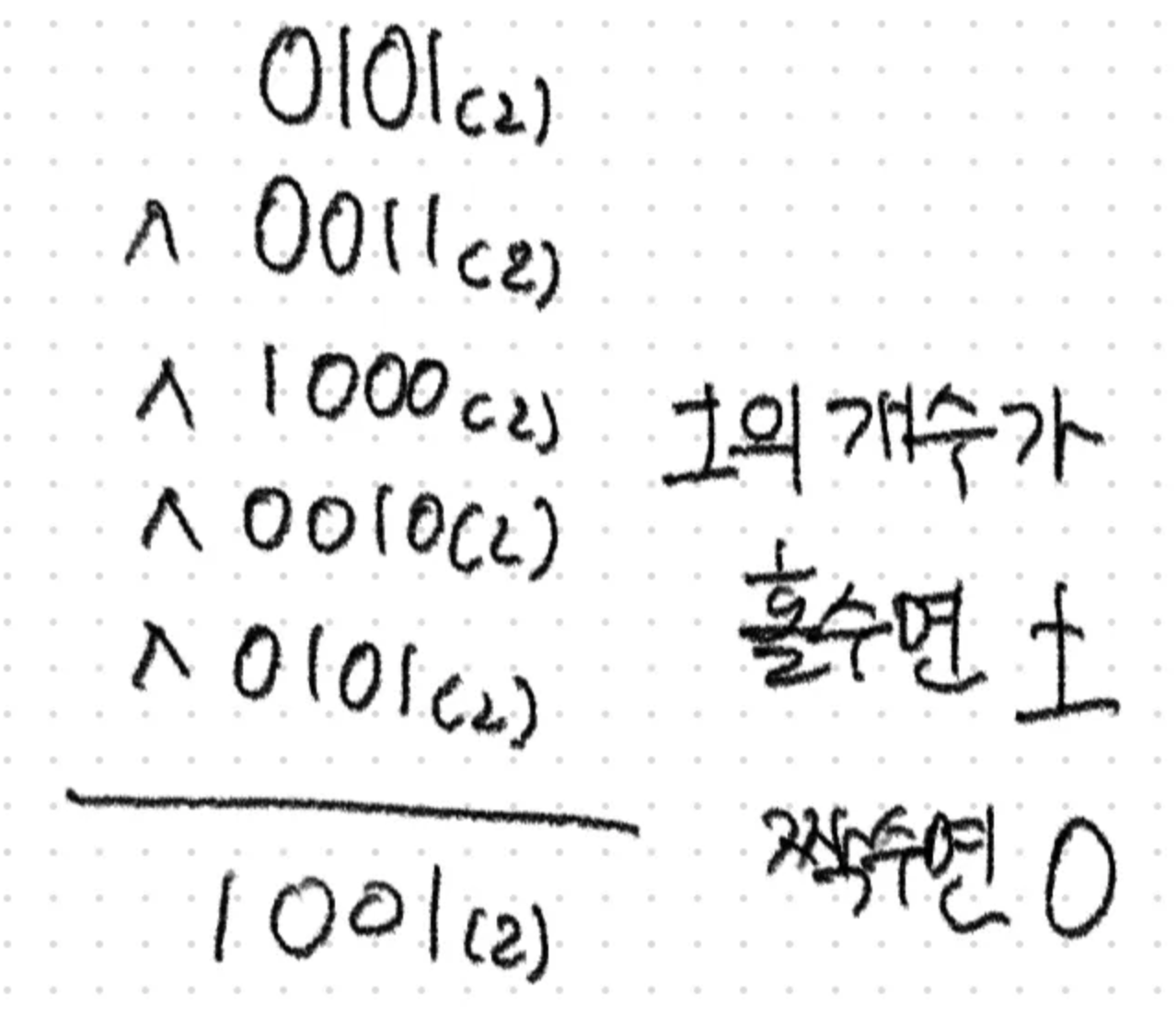
아래 처럼 이진수를 변환하여 계산을 하면 9가 나오는것을 확인할 수 있다.

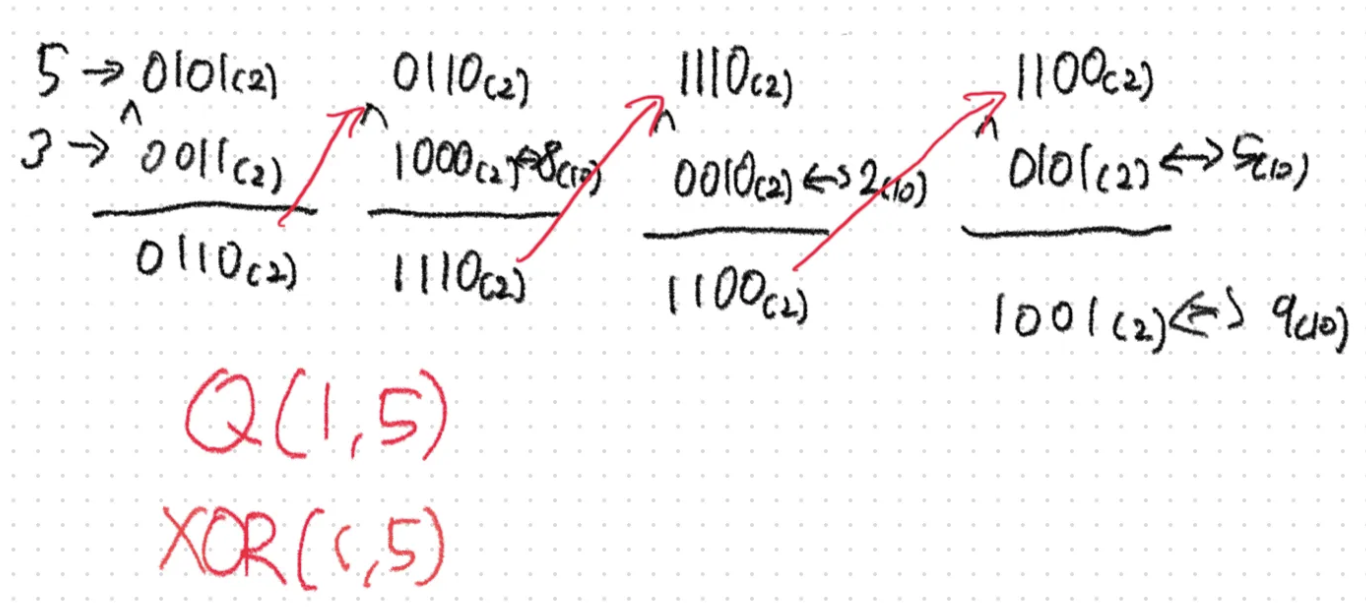
이 때, 하나하나씩 계산 하여도 되지만 한번에 모두 계산을 할 수 있다.

한 자리씩 볼때 1의 개수가 홀수이면 1, 짝수이면 0이 나온다.

누적합 배열을 적용할 수 있는 연산은?

누적합 배열은 모든 연산에 적용은 할 수 없다.

어떤 종류의 연산에 적용을 할 수 있냐면 바로 복원 작업이 가능한 연산이다.

교환 법칙과 결합법칙이 성립하여 역원이 존재하는 연산은 복원이 가능하다.

이것이 무슨 말인지 확인해보자.

• 교환법칙
  • 연산 기호 양쪽의 수의 자리를 바꿔서 계산해도 계산 결과가 같은 성질이다.
  • A * B = B * A
  • A + B = B + A
• 결합법칙
  • 세 수 이상의 연산에서 연산의 순서를 바꿔도 계산 결과가 같다.
  • A + B = C에서 B를 이행하면 A = C - B가 되는 것.
  • (A * B) * C = A * (B * C)

이런 법칙이 성립하는 연산은 구간 XOR 연산과 구간 곱셈 연산이다.

XOR 연산의 역원은?

누적합 배열을 이용해서 구간합을 구하려면 end의 누적합 배열에서 start-1 누적합 배열을 역원을 해야한다.

그렇다면 XOR의 역원을 알아야 하는데 XOR의 역원은 XOR이다.

왜 그런지 알아보자. 1011(2)를 1111(2)와 XOR 계산을 하면 0100(2)가 나오는데 이것을 다시 1011(2)랑 XOR하면 1111(2)가 나온다. 어떤한 A값을 자기와 같은 수 A와 XOR을 하면 무조건 0000이 나온다.

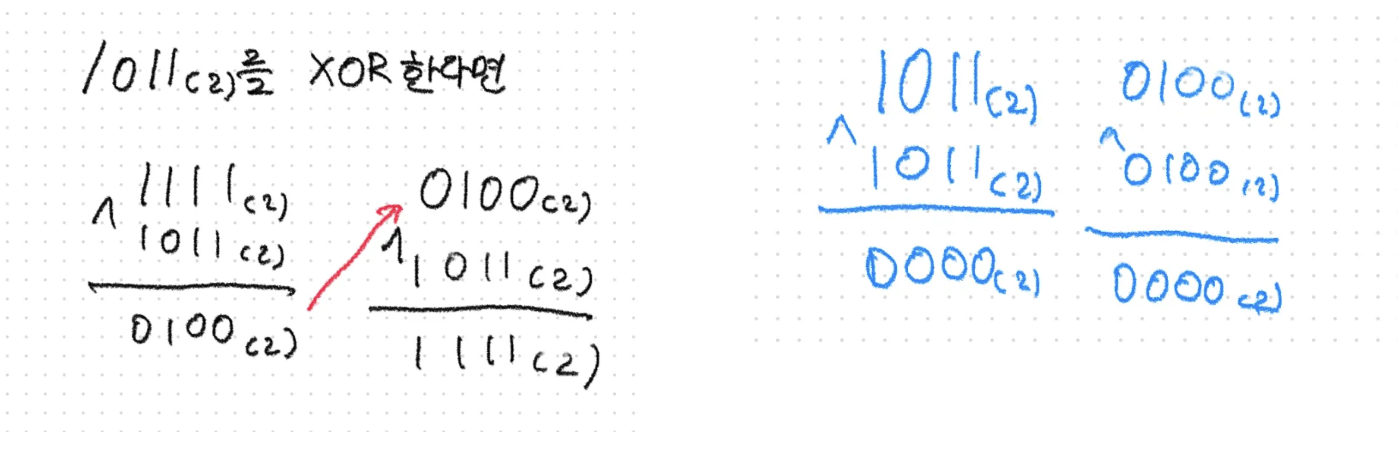
1. 누적XOR 배열 만들기

        // 1. 누적XOR 배열 만들기
        int[] acc = new int[N + 1];
        for (int i = 1; i <= N; i++)
            acc[i] = acc[i - 1] ^ arr[i];

2. Q번의 [s:e] 질문에 대해 누적XOR 배열을 사용해 구간XOR을 구한다.

3. 모든 구간XOR을 XOR한다.

        // 2. Q번의 [s:e] 질문에 대해 누적XOR 배열을 사용해 구간XOR을 구한다.
        int ans = 0;
        while (M-- > 0) {
            int i = sc.nextInt();
            int j = sc.nextInt();
            // 3. 모든 구간XOR을 XOR한다.
            ans ^= acc[j] ^ acc[i - 1];
        }
        System.out.println(ans);

전체코드

import java.util.Scanner;

class Main
{
    public static void main (String[] args) {
        Scanner sc = new Scanner(System.in);
        
        // 0. 입력받기
        int N = sc.nextInt();
        int M = sc.nextInt();
        int[] arr = new int[N + 1];
        for (int i = 1; i <= N; i++)
            arr[i] = sc.nextInt();

        // 1. 누적XOR 배열 만들기
        int[] acc = new int[N + 1];
        for (int i = 1; i <= N; i++)
            acc[i] = acc[i - 1] ^ arr[i];
        
        // 2. Q번의 [s:e] 질문에 대해 누적XOR 배열을 사용해 구간XOR을 구한다.
        int ans = 0;
        while (M-- > 0) {
            int i = sc.nextInt();
            int j = sc.nextInt();
            // 3. 모든 구간XOR을 XOR한다.
            ans ^= acc[j] ^ acc[i - 1];
        }
        System.out.println(ans);
    }
}

시간복잡도

이 알고리즘의 시간복잡도는 누적XOR 배열을 만들 때 O(N)

Q개의 쿼리 만큼 반복하여 계산을 하니 O(Q) 즉, O(N+Q)이다.