시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 | 128 MB | 27460 | 9311 | 6473 | 30.856% |
문제
N개의 정수로 이루어진 수열 A[1], A[2], …, A[N]이 있다. 이 수열에서 두 수를 골랐을 때(같은 수일 수도 있다), 그 차이가 M 이상이면서 제일 작은 경우를 구하는 프로그램을 작성하시오.
예를 들어 수열이 {1, 2, 3, 4, 5}라고 하자. 만약 M = 3일 경우, 1 4, 1 5, 2 5를 골랐을 때 그 차이가 M 이상이 된다. 이 중에서 차이가 가장 작은 경우는 1 4나 2 5를 골랐을 때의 3이 된다.
입력
첫째 줄에 두 정수 N, M이 주어진다. 다음 N개의 줄에는 차례로 A[1], A[2], …, A[N]이 주어진다.
출력
첫째 줄에 M 이상이면서 가장 작은 차이를 출력한다. 항상 차이가 M이상인 두 수를 고를 수 있다.
제한
- 1 ≤ N ≤ 100,000
- 0 ≤ M ≤ 2,000,000,000
- 0 ≤ |A[i]| ≤ 1,000,000,000
문제풀이
이 문제는 N개의 정수 수열에서 두 수의 차이가 M 이상이면서 가장 작은 쌍을 구하는 문제이다.
- 같은 숫자를 선택할 수 있고, 답은 항상 존재한다
아래 이미지를 보면 두 수의 차가 M 이상이면 정답이 가능하고 그 중 가장 작은 차가 정답이다.

가장 간단한 풀이는 모든 쌍을 반복하면서 계산을 하면 구할 수 있을것이다.. 하지만 이건 시간초과각 발생할 것이다.
새로운 예제를 보고 어떻게 문제 풀이를 진행할 것 인지 확인해보자.
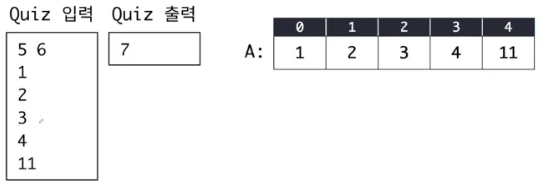
위의 이미지는 6이상이면서 가장 작은 값을 구하는 것이다.
한 번 씩 모두 비교해보자. 아래 이미지를 보면 가장 작은 값은 7이다.
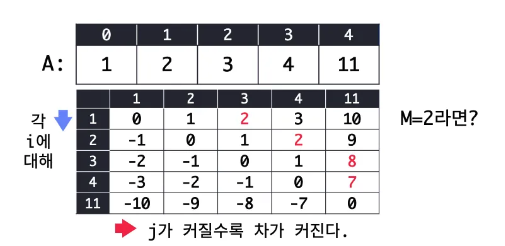
정렬을 했을때 즉 Aj -Ai ≤Aj+1 –Ai 임을 이용하여 Aj –Ai가 M 이상이면서 가장 작은 값을 Binary Search를 통해 찾을 수 있다.
이분 탐색 방법
for(int i = 0; i < N; i++) {
int l = i, r = N - 1;
while (l <= r) {
int m = (l + r) / 2;
int diff = arr[m] - arr[i];
if (diff > M) {
ansDiff = Math.min(ansDiff, diff);
r = m - 1;
}
else l = m + 1;
}
}
Ai-1 ≤ Ai 이므로 Ai와 차이가 M 이상이 되는 경계 Aj는 Ai-1의경계 Aj-1 보다같거나 큰범위에 있음을이용하면 매번 모든 범위를 보는게 아닌 이전 조사에 사용된 값을 다시 보지 않도록 Two Pointer를 적용할 수 있다.
투 포인터 풀이
Ai가 증가하는 방향이라도 쌍이 되는 경계 Aj도 증강하는 방향으로 이동한다.
int ansDiff = arr[N - 1] - arr[0];
int rightIndex = 0;
Aj 는 항상 Ai와의 M 이상이 되는 경계를 차가 유지한다. 마지막 원소까지 증가한다면 더 이상 이동하지 않는다.
while (arr[rightIndex] - arr[leftIndex] < M && rightIndex < N - 1)
rightIndex++;
AJ와 Ai의 차가 M 이상이면서 가장 작은 쌍의 값을 답에 반영한다.
int diff = arr[rightIndex] - arr[leftIndex];
if (diff >= M) ansDiff = Math.min(ansDiff, diff);
반복문을 돌며 증가한 Ai에 맞춰 j를 알맞은 경계로 이동한다.
for (int leftIndex = 0; leftIndex < N; leftIndex++) {
while (arr[rightIndex] - arr[leftIndex] < M && rightIndex < N - 1)
rightIndex++;
int diff = arr[rightIndex] - arr[leftIndex];
if (diff >= M) ansDiff = Math.min(ansDiff, diff);
}
전체코드
import java.util.*;
class Main
{
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int[] arr = new int[N];
for (int i = 0; i < N; i++)
arr[i] = sc.nextInt();
Arrays.sort(arr);
int ansDiff = arr[N - 1] - arr[0];
int pairIndex = 0;
for (int i = 0; i < N; i++) {
while (arr[pairIndex] - arr[i] < M && pairIndex < N - 1)
pairIndex++;
int diff = arr[pairIndex] - arr[i];
if (diff >= M) ansDiff = Math.min(ansDiff, diff);
}
System.out.println(ansDiff);
}
}
시간복잡도
투 포인트는 O(N)이지만 Sort를 사용하였기에 O(NlogN)을 더해야 한다.
즉, O(NlogN)이다.
'알고리즘 > Two Pointer' 카테고리의 다른 글
| [코딩테스트] [16472] 고냥이 (1) | 2025.01.03 |
|---|---|
| [코딩테스트] [17609] 회문 & [15831] 준표의 조약돌 (0) | 2024.12.31 |
| [코딩테스트] [11728] 배열 합치기 (0) | 2024.12.30 |
| [코딩테스트] [12891] DNA비밀번호 & [2118] 두개의탑 (0) | 2024.12.29 |
| [코딩테스트] [Two Pointer] [2003] 수들의 합 2 & [1806] 부분합 (0) | 2024.12.24 |
