728x90
1강 플레이그라운드 살펴보기
데이터 구조의 중요성
- 효율성
- 유지 보수성
- 확장성
- 데이터 활용을 위한 체계화 방법 (데이터의 공유,유지,정렬,검색 등)
데이터 구조 + 알고리즘 = 프로그램
- 데이터 추상화(abstraction)기법
- 데이터가 지닌 복잡성을 관리하기 위한 기술
- 데이터 구조를 디자인
- 추상화를 사용하는 이유 내부의 구현방식을 몰라도 되도록 하기 위함, 개발자는 더욱 쉽게 사용할 수 있다.
- 문제를 해결하기 위한 패턴
스위프트 REPL
- 스위프트 컴파일러(Read-Eval-Print-Loop)
- 즉시 코드를 실행하고 결과를 도출
- 값을 별도로 할당하지 않았을때 REPL이 직접 $R0라는 변수를 생성해서 값을 할당
기본적인 데이터 구조
- 배열 & 포인터
- 인접 데이터 구조: 데이터 메모리 영역중 인접한 부분에 저장(ex. 배열,힙,매트릭스,해시 테이블)
- 연결 데이터 구조: 서로 명확히 구분되는 메모리 영역을 차지하되 포인터라는 주소 체계로 연결, 관리 되는 구조(ex. lists, trees, graphs)
인접 데이터 구조(Contiguous data structures)
- 선형 데이터 구조(one-dimensional array), 일정한 순서에 따라 개별 데이터 요소에 접근하는 인덱스 기반 데이터 구조
배열
- 선형 배열(일차원 배열), 임의로 특정 요소에 접근할 수 있는 데이터 집합의 성질을 나타냄.
- 다차원 배열
- 행렬(matrix) : 2차원 배열을 구현

배열 선언
- Array<Type>형식 사용
- 축약형인 [Type]형식을 사용
- 명시적으로 선언하지 않고 컴파일러가 추측(type inference)하게 하는 방법
- var myIntArray : [Int] = [] 배열요소가 없는 배열 선언
- var my2DArray: [[Int]] = [[1,2],[10,11],[20,30]] 이차원 배열
배열 요소 가져오기
- 배열 내부의 요소를 가져오는 방법은 여러가지
- 해당 요소의 인덱스 번호를 안다면 직접 호출 가능
- 순환문을 이용해서 특정 요소를 반복적으로 가져와야 할 때 for…in 문법을 사용
- 일정 영역에 속한 요소를 가져와야 할 때도 있는 범위를 지정해서 가져온다.
//1차원 배열에서 반복적으로 가져오는 방법
var myIntArray = [1,2,3,4,5]
for element in myIntArray {
print(element)
}
//2차원 배열에서 특정 배열 요소를 직접 가져오는 방식
var my2DArray: [[Int]] = [[1,2],[10,11],[20,30]]
my2DArray: [[Int]] = 3 values {
[0] = 2 values {
[0] = 1
[1] = 2
}
[1] = 2 values {
[0] = 10
[1] = 11
}
[2] = 2 values {
[0] = 20
[1] = 30
}
}
2> var element = my2DArrau[0][0]
element: Int = 1
3> element = my2DArray[1][1]
4> print(element)
배열 요소 추가
- 추가를 맨 앞, 끝 부분에 인지 따라 달라진다.
- 맨 끝 부분에 요소를 추가하는 방법
- .append 사용, myIntArray.append(10)
- 특정 인덱스 위치에 요소 삽입
- .insert 사용, myIntArray.insert(5, at: 2)
배열 요소 삭제
- 배열 요소의 추가와 마찬가지로 삭제하려는 요소의 위치가 어떤 부부인지에 따라 달라진다
- 맨 끝 요소를 삭제하는 방법
- .removeLast, myIntArray.removeLast()
- 특정 요소를 삭제하는 방법
- .remove(at), myIntArray.remove(at: 3)
연결 데이터 구조(Linked data structures)
- 데이터 타입과 이를 다른 데이터와 묶어주는 포인터(메모리상의 위치 주소)로 구성
- Swift는 직접적으로 포인터에 접근하지 않으며, 포인터를 활용할 수 있는 별도의 추상 체계 제공
- 연결리스트
- 데이터와 다음 노드에 연결할수 있는 정보를 포함
- 추가 링크 정보를 통해 연결된 데이터에서 앞 또는 뒤로 이동,
- 추가 노드를 삽입하거나 삭제하는 일은 매우 간단
- 자체 참조 클래스인 노두로 구성,각각의 노드는 데이터와 전체 연결데이터에서 다음 노드로 이동할 수 있는 링크 정보를 포함
- S: 단일연결리스트, N: 단일연결리스트의 마지막부분, D: 이중연결리스트 좌측(이전의 노드), 우측(다음노드)

단일 연결 리스트와 이중 연결 리스트 구조 비교
단일 연결 리스트
- 연결 리스트 데이터 구조는 앞서 정의한 네 개의 속성으로 구성,
class LinkedList<T> {
var item
var next: LinkedList<T>?
}
데이터 구조의 종류와 장단점
데이터 구조 장점 단점
| 배열 | 인덱스 값을 알고 있는 경우 | |
| 데이터 접근 신속, 삽입도 신속 | 크기가 고정되고 삭제 및 검색은 느리게 진행! | |
| 정렬된 배열 | 비정렬 배열에 비해 검색속도가 빠름 | 크기가 고정되고, 삭제 및 검색 또 조심 |
| 큐 | 먼저 입력된 데이터가 먼저 출력 될 수 있는 FIFO 접근 방식이 제공 | 다른 요소에 대한 접근 속도가 느리다. |
| 스택 | 나중에 입력된 데이터가 먼저 출력 될 수 있는 LIFO 접근 방식이 제공 | 다른 요소에 대한 접근 속도가 느리다. |
| 리스트 | 데이터 삽입 및 삭제속도가 빠르다 | 검색 속도 가 느리다. |
| 해쉬 테이블 | 키값을 아는 경우 | |
| 신속 접근, 새로운 요소 삽입 | 키값을 모를 경우 접근 속도가 느리고, 삭제 속도가 느리며 메모리 효율성이 떨어진다. |
데이터 구조 장점 단점
| 힙 | 매우 신속하게 삽입 및 삭제가 가능, | |
| 최대or최소에 대한 접근 속도 빠름 | 다른 요소에 대한 접근 느림 | |
| 트라이 | 데이터 접근 속도 빠름, | |
| 서로 다른 키값 충돌 X | ||
| 삽입,삭제 신속 | ||
| 문자열 딕셔너리 정렬,프리픽스 검색 유용 | 특정 상황에서 해시 테이블보다 속도가 느림. | |
| 이진 트리 | (균형 잡힌 트리구조일때)삽입, 삭제,검색 속도가 매우 빠르다. | 삭제 알고리즘 작성이 복잡, 트리구조가 삽입 순서에 영향, 성능이 저하 |
| 레드블랙 트리 | 삽입,삭제,검색 속도 매우 빠름, | |
| 트리는 항상 균형 상태 유지 | 한계 상황에서 데이터 구조를 운영하므로 구현이 까다로움 | |
| R 트리 | 공간적 데이터를 나타낼때 good, | |
| 2차원 이상 구조를 지원 | 성능 검증 X | |
| 그래프 | 실제 세계의 상황을 반영한 모델 구현 | 일부 알고리즘은 느리고 복잡 |
알고리즘 개요
알고리즘 구현을 위한 자원이 매우 희박한 상태
알고리즘을 작성하려면 시간과 공간이 필요, 이 두가지가 가장 중요한 자원
문제의 규모를 측정할 때 함수의 점근 행동(asymptotic behavior)에 관심을 갖는다.
점근행동
- 두 개 알고리즘 기법을 비교하는 기초자료
- 문제 해결을 위한 함수의 크기가 커지는 속도보다 자원의 소모의 속도가 느리게 증가하는가를 확인
좋은 알고리즘이라면 규모가 큰 문제일수록 신속하게 해결
데이터 구조에서는 필수적으로 파악할 내용
- 새로운 데이터 아이템을 삽입하는 방법
- 데이터 아이템을 삭제하는 방법
- 특정 데이터 아이템을 찾는 방법
- 모든 데이터 아이템을 순회 하는 방법
- 데이터 아이템을 정렬하는 방법
스위프트에서의 데이터 타입
원천 데이터 타입이라고 하면 단일 값을 지니는 스칼라 타입을 일컫는 경우가 많다.
대표적인 스칼라 타입 데이터 하지만 Swift는 아님
- int
- float
- double
- char
- bool
스위프트에서 제공 하는 원천 데이터 타입
밸류 타입과 레퍼런스 타입
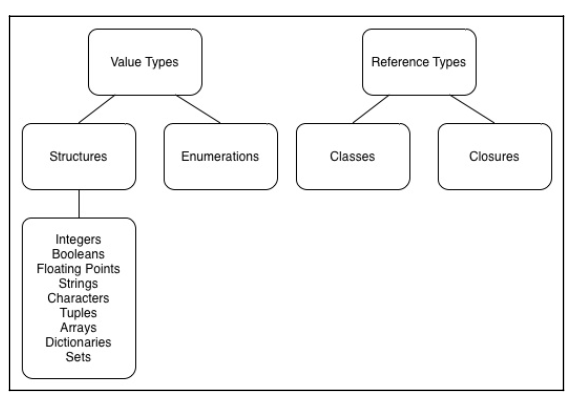
밸류 타입(value types)
- 오직 하나의 소유 객체만을 지님,
- 타입의 데이터가 변수or상수에 할당됐을 때 or 함수에 전달됐을 때, 지니고 있는 값 복사
- 구조체와 열거형, 스위프트의 모든 데이터 타입은 기본적으로 구조체
레퍼런스 타입(reference types):
- 값을 복사하지 않고 공유
- 변수에 할당하거나, 함수에 전달할 때 동일한 인스턴스를 참조값으로 활용
- 여러 개의 소유 객체가 참조라는 방식으로 공유
기명 타입과 복합 타입
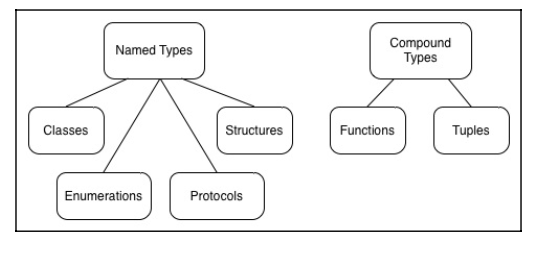
기명 타입(named types)
- 사용자가 정의할 수 있는 데이터 타입
- 해당 타입이 정의될 당시 특정한 이름을 부여할 수 있는 타입
- 클래스, 구조체, 열거형, 프로토 타입
- 배열, 딕셔너리, 세트, 옵셔널 값을 나타낼 수 있는 기명타입 별도로 마련
- 익스텐션 선언을 통해 동작범위 확장
복합 타입(compound types)
- 별도 이름이 붙여지지 않는 타입
- function 타입과 type 타입등 두개의 복합 타입이 정의
- 기명 타입은 물론 다른 복합 타입을 포함 가능
- 튜플 타입은 두개의 요소를 포함, 첫번째 Int(기명타입), (Float,Float)라는 복합 타입(Int(Float,Float))
타입 에일리어스
- 기존의 타입을 또 다른 이름으로 부를 수 있는 방법
- typealias TCPPacket = UInt16
- 타입 에일리어스를 정의한 뒤에는 언제든지 어디서든지 해당 이름으로 원본 타입 사용
스위프트 표준 라이브러리의 컬렉션 타입
- 세트
- 딕셔너리
- 배열
정식은 아니지만 튜플도 있음, 튜플에서 정렬된 값은 어떤 타입 가능
점근적 분석
- 무한대에 가까운 입력값을 분석하는데 걸리는 시간을 측정하는 방법을 점근적 분석
- 서비스를 개발 할때 원하는 정보를 신속하게 찾아내는 일은 중요
- 알고리즘이 최적의 성능을 낼 수 있는지 확인하기 위해 알고리즘 실행 속도 측정
- 점근적 분석을 통하여 얻을 수 있는 것
- 데이터가 폭주하는 상황이라면, 얼마 만큼의 저장공간이 필요한가?
- 알고리즘이 특정 규모의 입력값을 처리하는데 걸리는 시간은 얼마인가?
- 과연 그 문제를 해결할 수 있는가?
- 예시
- 숫자 목록 정렬 함수의 실행 시간 분석 할 때, 입력 데이터 크기에 따라 함수의 실행 시간이 얼마나 길어지는지 알아야함
데이터 크기 분석 방법
- 점근적 분석을 통해 상수의 변화와 무관하게, 선형 로그식인 병합형 정렬 알고리즘이 삽입형 정렬 알고리즘 보다 빠르다는 것을 알게됨.
- 실행환경이 동일한 경우에만 정확하게 측정 가능, 이러한 이유로 시간 측정에서 상수를 무시하는 경우가 대부분
- Computer Science에서 빅오는 함수의 점근적 분석을 표현하는 가장 대표적인 방법 중 하나
- 알고리즘 표현에서 상수를 감춤으로써 좀 더 간편하게 실행 속도를 측정할 수 있음.
- 빅오는 외부 경계선, 즉 성장의 순서를 비교. 이때 외부경계선은 해당 알고리즘이 분석을 완전히 마치기까지 걸리는 최대 시간을 의미
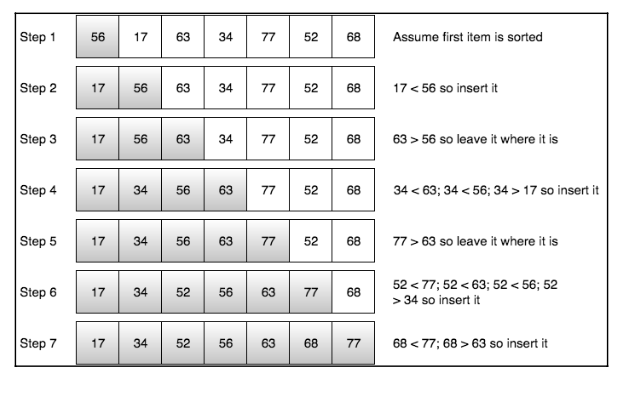
삽입형 정렬 알고리즘 작동 원리
- 1단계, 아이템은 정렬 순서대로 놓여 있다고 가정
- 2단계, 두번째 아이템과 바로 앞 아이템의 크기를 비교하는데, 두 번째 아이템이 더 작은 경우 위치를 서로 바꾼뒤 다시 맨 앞이동
- 3단계, 동일한 패턴 반복
// 삽입형 정렬 알고리즘 func insertionSort( alist: inout [Int]){ for i in 1..<alist.count { let tmp = alist[i] var j = i - 1 while j >= 0 && alist[j] > tmp { alist[j+1] = alist[j] j = j - 1 } alist[j+1] = tmp } }
- 점근적 판단에서 함수 f가 $x^2$의 이차방정식보다 빠르게 증가할 수 없음을 나타냄
- 함수 f의 실행시간이 가장 오래 걸리때가 바로 $O(x^2)$라고 하는데 최악의 상황에서 실행되도 $O(x^2)$보다 작다는 뜻이다.
병합형 정렬 알고리즘 구현 방식
func mergeSort<T:Comparable>( list:inout [T]) {
if list.count <= 1 {
return
}
func merge( left:[T], right:[T]) -> [T] {
var left = left
var right = right
var result = [T]()
while left.count != 0 && right.count != 0 {
if left[0] <= right[0] {
result.append(left.remove(at: 0))
} else {
result.append(right.remove(at: 0))
}
}
while left.count != 0 {
result.append(left.remove(at: 0))
}
while right.count != 0 {
result.append(right.remove(at: 0))
}
return result
}
var left = [T]()
var right = [T]()
let mid = list.count / 2
for i in 0..<mid {
left.append(list[i])
}
for i in mid..<list.count {
right.append(list[i])
}
mergeSort(list: &left)
mergeSort(list: &right)
list = merge(left: left, right: right)
}
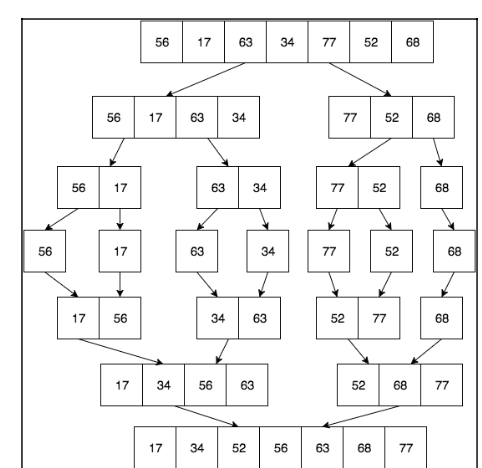
- 가장 먼저 하는 일은 배열을 분할 하는 것
- 아이템의 수를 반으로 나누고 반복하여 배열의 아이템 수가 하나 될 때까지 반복 실행
- 그 다음, 숫자 비교 하면서 배열을 합침
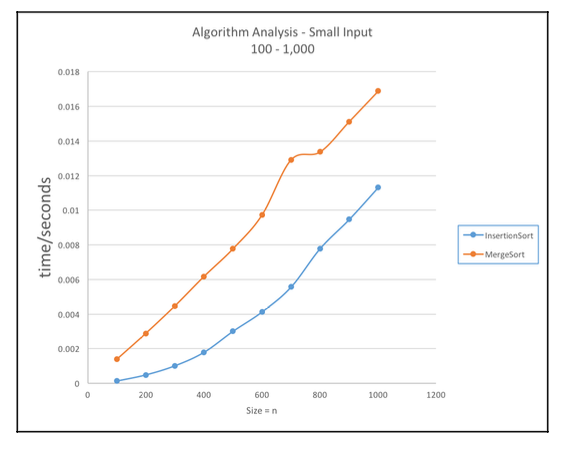
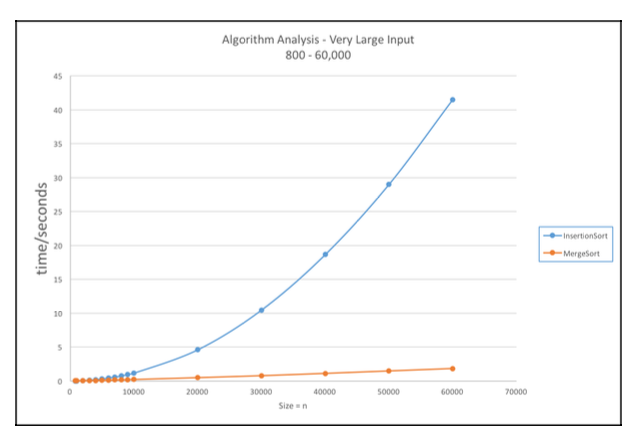
- 소규모 입력 데이터에서는 삽입형 정렬 알고리즘이 병합형 정렬 알고리즘에 비해 더 나은 성능을 냄
- 반면 대규모 입력 데이터에서는 병합형 정렬 알고리즘이 삽입형 정렬 알고리즘에 비해 훨씬 더 나은 성능을 냄.
- 입력 데이터가 증가할 수록 실행 속도 차이가 많이 남.
728x90
'Swift > 정리' 카테고리의 다른 글
| [SwiftDataStructure&Algorithms] 기본 데이터 구조(세트, 튜플) (0) | 2024.03.15 |
|---|---|
| [SwiftDataStructure&Algorithms] 기본 데이터 구조(배열, 딕셔너리) (0) | 2024.03.13 |
| XCODE IOS 프로파일링 디버깅 하는 방법 (1) | 2024.01.07 |
| [SwiftUI] 아키텍처 고민 (0) | 2024.01.06 |
| [SwiftUI] Combine - 기본 (0) | 2023.09.16 |